时间、空间复杂度分析

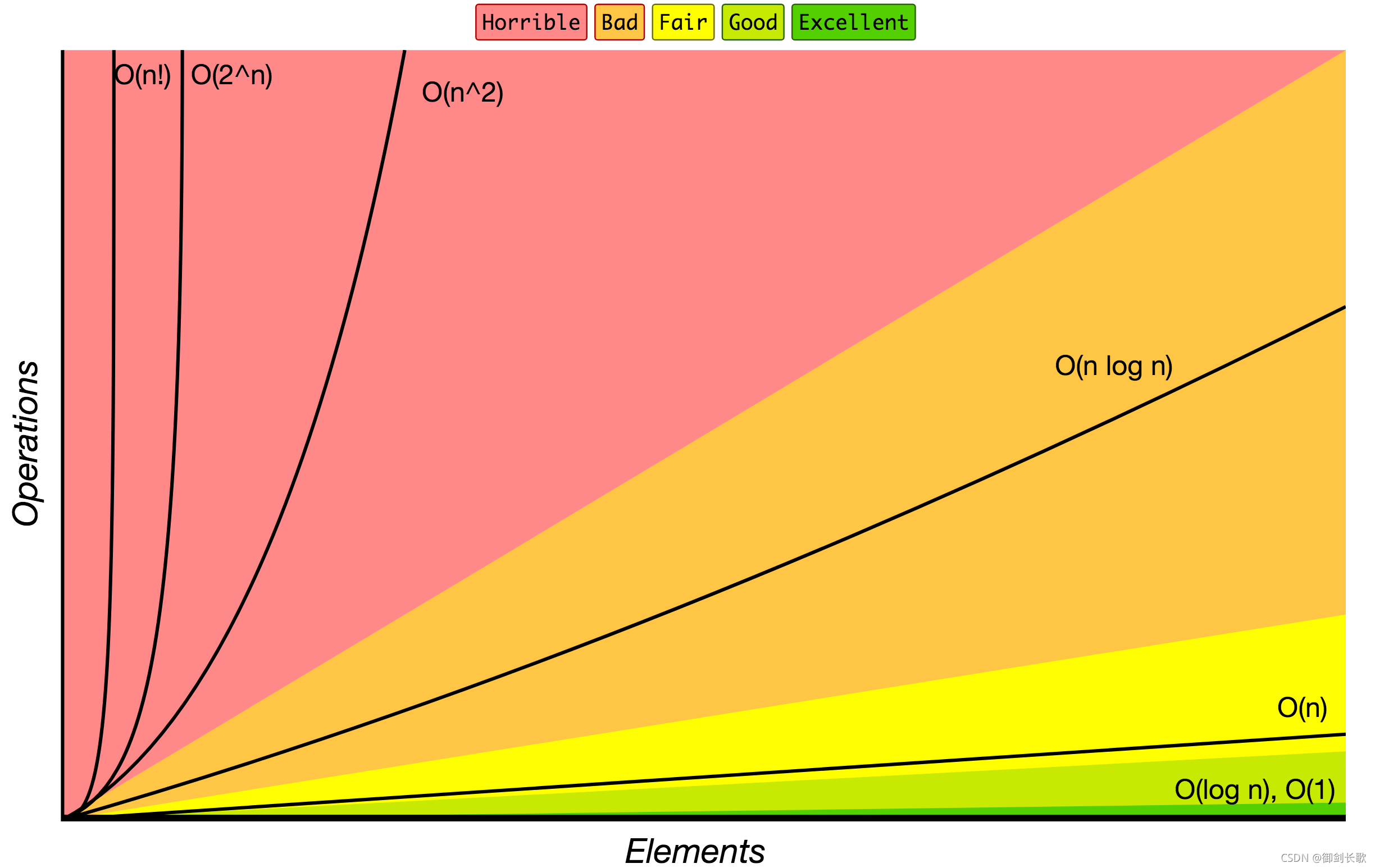
常用的七种时间复杂度

O(1): Constant Complexity 常数时间复杂度
O(log n): Logarithmic Complexity 对数复杂度
O(n): Linear Complexity 线性时间复杂度
O(n^2): N square  Complexity 平方
O(n^3): N square Complexity 立方
O(2^n): Exponential Growth 指数
O(n!): Factorial 阶乘

注意点:
不考虑常数系
只看最高复杂度的运算

O(1)

        int n  = 1000;
        System.out.println("hello"+n);

O(N)

        int n  = 1000;
        for (int i = 0; i < n; i++) {
            System.out.println("hello"+n);
        }

ps: 加入并列的 for 循环 时间复杂度还是 O(N)
O(N^2)

        int n  = 1000;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.println("hello"+n);
            }
        }

O(log(n))

        int n = 1000;
        for (int i = 1; i < n; i = i * 2) {
            System.out.println("hello" + n);
        }

O(k^n)

    public int fib(int n) {
        if (n < 2) {
            return n;
        }
        return fib(n - 1) + fib(n - 2);
    }

时间复杂度曲线图

递归的时间复杂度

构造递归树
通过缓存，排除重复
常用算法中的应用

空间复杂度

数组的长度
如果代码中开了数组，那么数组的长度基本上就是代码的空间复杂度
如果开了一维数组，数组的长度是 n，空间复杂度基本上就是 O(n)
如果开了二维数组，数组的长度是 n 平方，空间复杂度基本上就是 O(n^2)
递归的深度
递归最深的深度，就是空间复杂度的最大值