2017蓝桥C语言 5.标题： 杨辉三角

标题： 杨辉三角

杨辉三角也叫帕斯卡三角，在很多数量关系中可以看到，十分重要。

第0行：           1
第1行：          1 1
第2行：         1 2 1
第3行：        1 3 3 1
第4行：       1 4 6 4 1

…

两边的元素都是1， 中间的元素是左上角的元素与右上角的元素和。

我们约定，行号，列号都从0计数。
所以： 第6行的第2个元素是15，第3个元素是20

直观地看，需要开辟一个二维数组，其实一维数组也可以胜任。
如下程序就是用一维数组“腾挪”的解法。

// 杨辉三角的第row行，第col列 
long long f(int row, int col){
	if(row<2) return 1;
	if(col==0) return 1;
	if(col==row) return 1;
	
	long long a[1024];
	a[0]=1;
	a[1]=1;	
	int p = 2;
	int q;
	
	while(p<=row){
		a[p] = 1;
		for( _________________ ) a[q] = a[q] + a[q-1]; //填空
		p++;
	}
	
	return a[col];
}

int main()
{
	printf("%d\n", f(6,2));
	printf("%d\n", f(6,3));
	printf("%lld\n", f(40,20));	
	return 0;
}

请仔细分析源码，并完成划线部分缺少的代码。
注意：只提交缺少的代码，不要提交已有的代码和符号。也不要提交说明性文字。

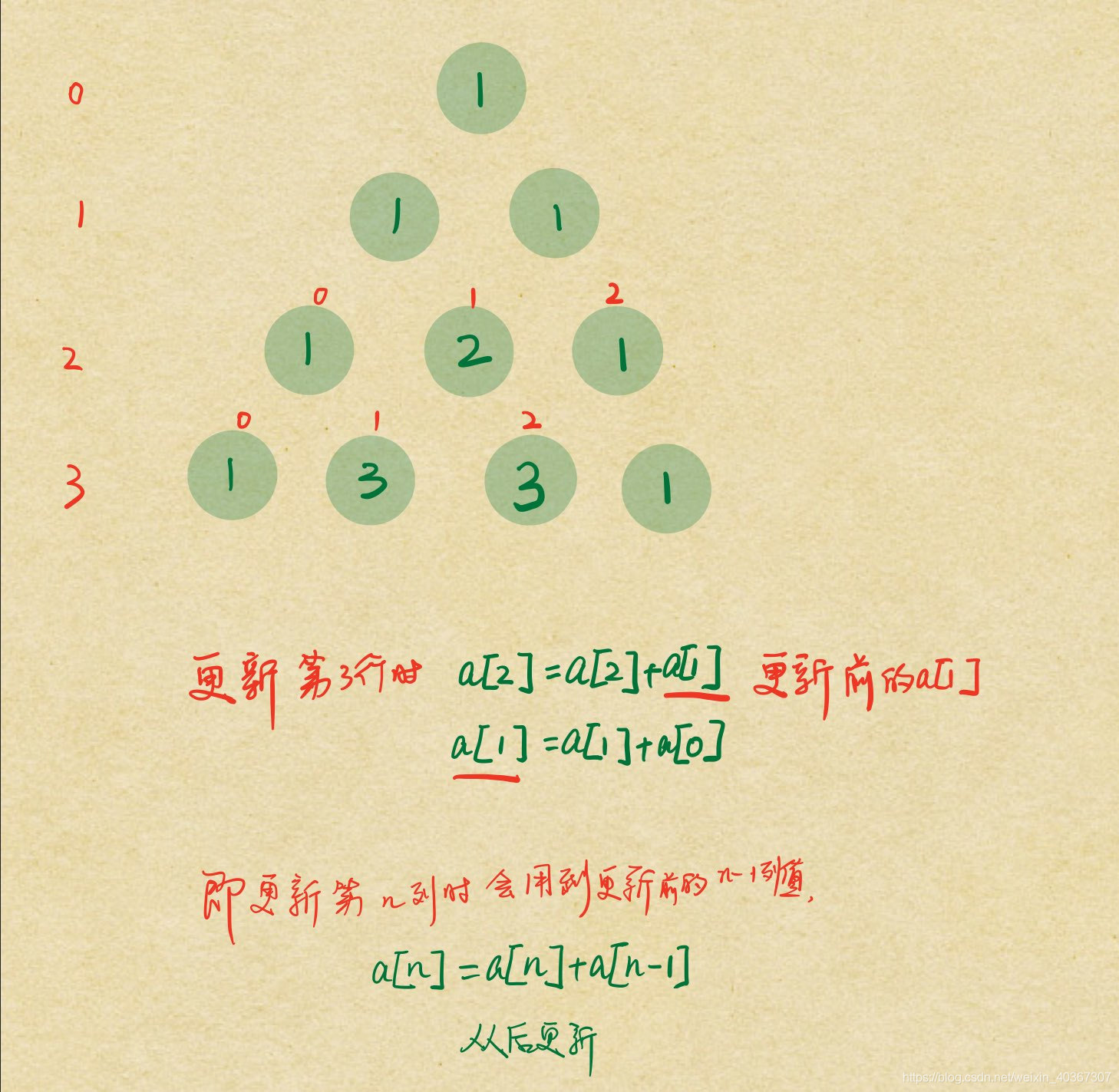
答案：q=p-1;q>0;q–
(动规，单数组从后)