机器学习复习(2)——神经网络

神经网络概述（BP推导）&CNN

神经网络

神经元模型

基本结构：

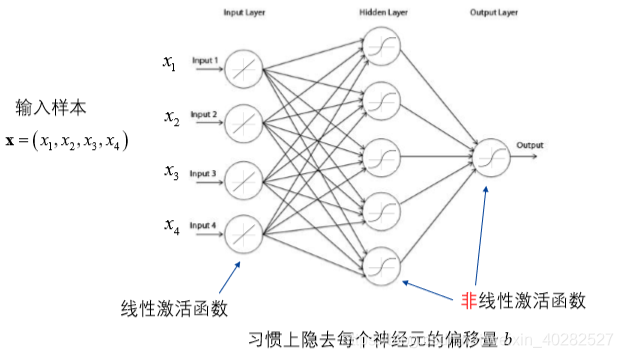
BP网络

三层神经网络的推导

• 标准的推导

  • 符号说明：

    • $W^l$表示$l$到$l+1$的权重矩阵，维数为：$l+1$的节点数$\times l$的节点数
    • $f$表示激活函数
    • $z^l$表示的是$l$层的输入$a^l$表示$l$的输出（即经过了激活函数）
    • 输入为一个样本（$b$个属性）

  • 前向计算（以三层网络为例）：

    • $z^{(2)}=W^{(1)}x+b^{(1)}$

    • $a^{(2)}=f(z^{(2)})$

    • $z^{(3)}=W^{(2)}x+b^{(2)}$

    • 更加普遍的：
      $$\begin{gathered} z^{(l+1)}=W^{(l)}{a}^{(l)}+b^{(l)} \\ {a}^{(l+1)}=f(z^{(l+1)}) \end{gathered}$$

    • 假设损失函数为$J$

  • 反向（梯度计算：矩阵形式）:

    • 每一层的梯度：${\delta }^{(l)}=(W^{(l)}{)}^T{\delta }^{(l+1)}⨀f^{\prime }(z^{(l)})$
    • 每一层的权重的梯度：${▽}_{W^{(l)}}={\delta }^{(l+1)}(a^{(l)}{)}^T$
    • 每一层的偏置的梯度：${▽}_{b^{(l)}}={\delta }^{(l+1)}$

  • 一些说明：

    • 最外层（包括损失函数的要单独处理）

    • $⨀$之对应元素相乘

    • $f$如果是对于每一个元素的操作，则对于内部的求导最终得到的矩阵维数不变。

      $f^{{}^{\prime }}([z^1,z^2,z^3])=[f^{{}^{\prime }}(z^1),f^{{}^{\prime }}(z^2),f^{{}^{\prime }}(z^3)]$

    • 如果原本前向计算的时候是：$z^{(l+1)}=(W^{(l)}{)}^T{a}^{(l)}+b^{(l)}$此时维数与开始相比是转置关系，同时最终求导得到的结果应该是整体转置。

  • 一些推导（根据单个元素的计算）

    • 对于$l$层的$i$个节点:${\delta }_i^{(l)}=({\sum }_{j=1}^{s_{l+1}}{W}_{ji}^{(l)}{\delta }_j^{(l+1)})f^{\prime }(z_j^{(l)})$
    • $\frac{\partial J}{\partial W_{ij}^{(l)}}={\delta }_i^{(l+1)}{a}_j^{(l)}$由此写出矩阵形式就是c.ii

学习算法流程：

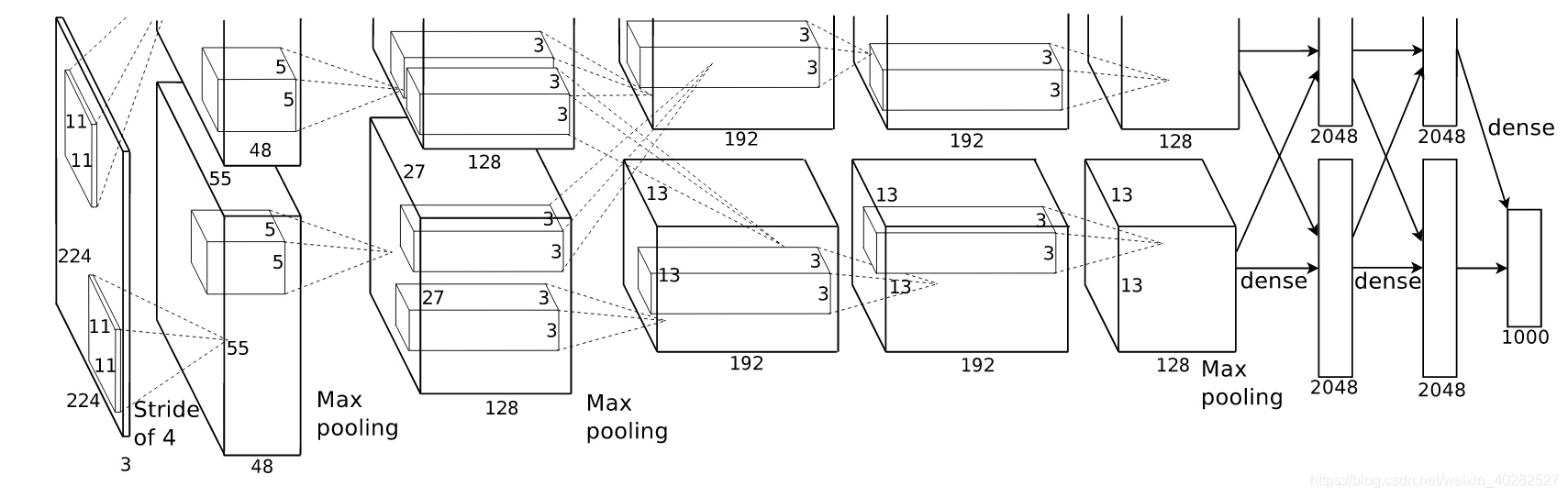
卷积神经网络

基本结构

• 卷积
• 池化
• 全连接

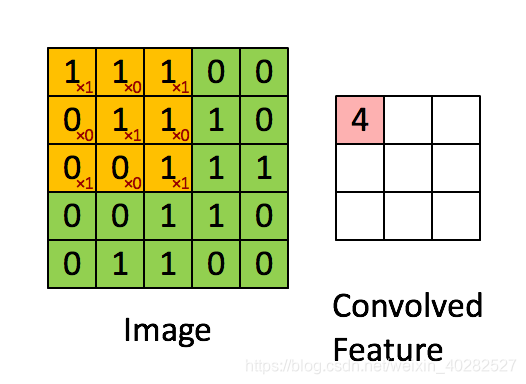
卷积神经网络的计算

• 上面的动图展示了一个$3\times 3$的核是如何操作的，实际上就是对应元素相乘再求和

• 一些理解：

  • 实际上这里的滤波可以类比简单信号的高频低频滤波，实际上都是对某一特定的信号有较高/较低的输出。（同神经网络的激活）

  • 一层一层的卷积实际上也是前面的实现低阶的特征，后面越来越高

  • 在图像中

    • rgb图中：width*height*depth(channel =3 some times)
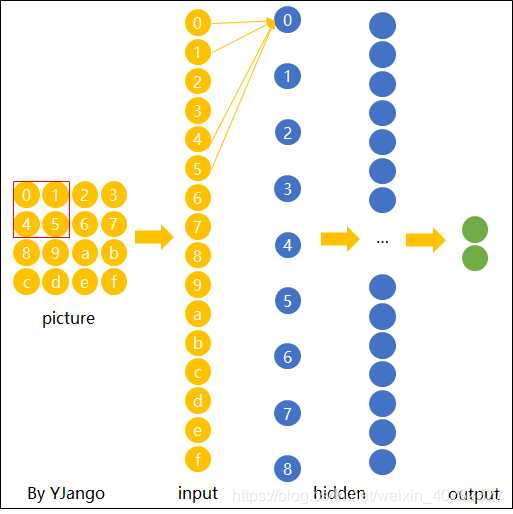
    • 因为需要图像保持不变性（一个图片中的特质出现在上面或者下面应该都能够识别）-卷积神经网络能够不同位置共享权重（如下图）
      
      

• 对于边缘的处理（希望能够保持和原本的图像数据一致）：zero padding 操作：即在卷积之前先进行以0填充周围一圈。

  • 计算说明：原尺寸$n\times n$卷积核$f\times f$ 如果不进行填充，卷积后：$n-f+1\times n-f+1$ 若先填充$p$层则，卷积后 $n+2p-f+1\times n+2p-f+1$只需满足$p=\frac{f-1}{2}$即可使前后尺寸不变

  • valid卷积是不填充，same是填充（具体实现中）

  • 多个filters时：提取多个特征（输出不再是depth=1）

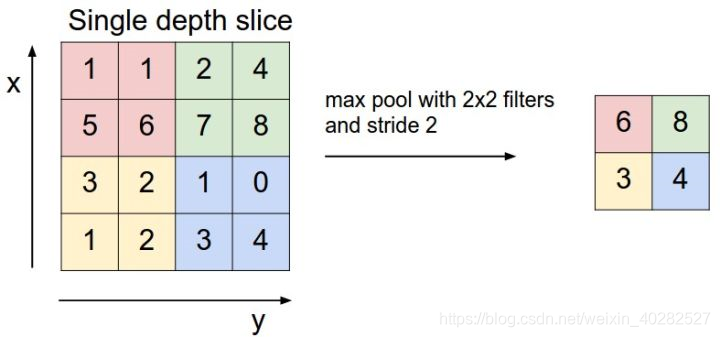
  • pooling：

---