Harris角点

        大部分搬运：http://www.cnblogs.com/ronny/p/4009425.html

一、理论知识

Harris角点是在1981的Moravec的角点理论的基础上再1988由Harris提出的。因此，先说明Moravec的角点理论。Moravec角点说明的从方向（1，0），（0，1），（1,1），（-1,1）四个方向出发的像素的变化值，它有三种情况： 

（1）如果图像是什么平坦的，那么像素的变化不大。

（2）如果图像是一条边，那么在沿这条边滑动时像素变化不大，而在沿垂直于这条边的方向滑动时，像素的变化会很大。 

（3） 如果图像是一个角点时，任何方向移动像素的值都会发生很大变化。

由于这个角点的判断只通过4个方向来说明，对方向的依赖性太强，因此，Harris考虑从各个方向出发来优化它。各个方向的话就需要引进微分的思想。在Moravec中判别的公式为

也就是在4个方向的像素差的平方和（还要乘以权值w）。那么在Harris角点中需要将4个方向变成各个方向。

I(u+Δx,v+Δy)=I(u,v)+I x (u,v)Δx+I y (u,v)Δy+O(Δx 2 ,Δy 2 )≈I(u,v)+I x (u,v)Δx+I y (u,v)Δy+ I(u+Δx,v+Δy)=I(u,v)+Ix(u,v)Δx+Iy(u,v)Δy+O(Δx2,Δy2)≈I(u,v)+Ix(u,v)Δx+Iy(u,v)Δy

自相关函数为：

其中：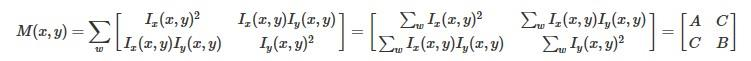

也就是说图像I(x,y) 在点(x,y)  处平移(Δx,Δy) 后的自相关函数可以近似为二项函数：

椭圆的扁率和尺寸是由M(x,y) 的特征值λ 1 、λ 2   决定的，椭圆的方向是由M(x,y) 的特征矢量决定的，如下图所示，椭圆方程为：

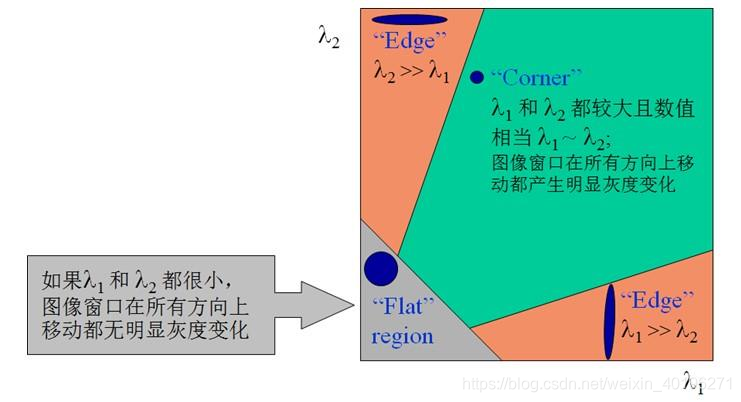
椭圆函数特征值与图像中的角点、直线（边缘）和平面之间的关系如下图所示。共可分为三种情况：

• 图像中的直线。一个特征值大，另一个特征值小，λ 1 ≫λ 2或λ 2 ≫λ 1 。自相关函数值在某一方向上大，在其他方向上小。
• 图像中的平面。两个特征值都小，且近似相等；自相关函数数值在各个方向上都小。
• 图像中的角点。两个特征值都大，且近似相等，自相关函数在所有方向都增大。

根据二次项函数特征值的计算公式，我们可以求M(x,y)  矩阵的特征值。但是Harris给出的角点差别方法并不需要计算具体的特征值，而是计算一个角点响应值R 来判断角点。R  的计算公式为：

式中，detM为矩阵M=[AB BC ] 的行列式；traceM  为矩阵M  的直迹；α  为经常常数，取值范围为0.04~0.06。事实上，特征是隐含在detM 和traceM 中，因为，

 

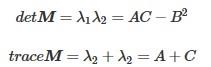
二、算法步骤

1. 计算图像I(x,y) 在X 和Y 两个方向的梯度I x 、I y   。

2. 计算图像两个方向梯度的乘积。

3.使用高斯函数对I 2 x 、I 2 y 和 Ixy 进行高斯加权（取σ=1  ），生成矩阵M 的元素A、B  和C  。

4.计算每个像素的Harris响应值R  ，并对小于某一阈值 t 的 R 置为零。

5. 在3×3 或5×5  的邻域内进行非最大值抑制，局部最大值点即为图像中的角点。

 

三、Harris性质

Harris角点检测算子对亮度和对比度的变化不敏感

这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

Harris角点检测算子具有旋转不变性

Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值R R 也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

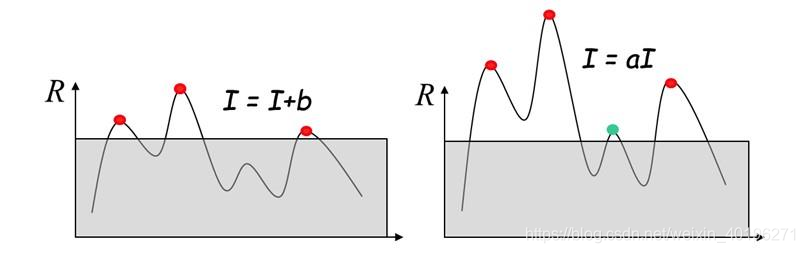
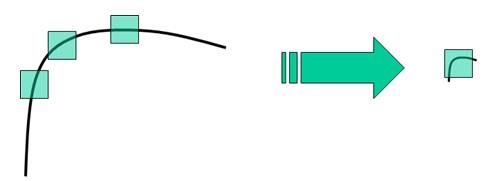
Harris角点检测算子不具有尺度不变性

如下图所示，当右图被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

四、多尺度Harris

由于Harris角点不具有尺度不变性，所以要想办法对它进行优化。

未完待续。。。。。。。。