【重磅】批量梯度下降、随机梯度下降、小批量梯度下降

最新推荐文章于 2025-06-03 10:35:44 发布

置顶挺烦先森

最新推荐文章于 2025-06-03 10:35:44 发布

阅读量756

点赞数

CC 4.0 BY-SA版权

分类专栏：模型算法相关

本文链接：https://blog.youkuaiyun.com/weixin_40166430/article/details/81155601

模型算法相关专栏收录该内容

6 篇文章

订阅专栏

本文介绍了三种梯度下降方法：批量梯度下降、随机梯度下降和小批量梯度下降，并对比了它们各自的优缺点及适用场景。此外还详细解释了梯度下降的基本原理及其在机器学习中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

梯度下降有三种

1. 批量梯度下降（Batch Gradient Descent，BGD）

2. 随机梯度下降（Gradient Descent，SGD）

3. 小批量梯度下降（Mini-Batch Gradient Descent，MBGD）

不同点在于损失函数使用的样本量的不同，其根本流程是一毛一样的啊！

各有优缺点。

方法	说明	优点	缺点	适用实例
批量梯度下降 BGD	最原始方法，每次跟新参数时，使用所有样本，即损失函数由所有样本构成。	1. 全局最优解； 2. 易于并行实现。	1. 样本多时，训练时间慢	样本量比较小
随机梯度下降 SGD	损失函数使用一个样本，噪声比BGD要多	1. 训练速度快	1. 准确度降低，经常非全局最优 2. 不易于并行实现	样本量比较大，或者在线学习算法
小批量梯度下降 MBGD	损失函数使用一部分样本	综合BGD、SGD	综合BGD、SGD	一般情况

方法

说明

优点

缺点

适用实例

批量梯度下降 BGD

最原始方法，每次跟新参数时，使用所有样本，即损失函数由所有样本构成。

1. 全局最优解；

2. 易于并行实现。

1. 样本多时，训练时间慢

样本量比较小

随机梯度下降 SGD

损失函数使用一个样本，噪声比BGD要多

1. 训练速度快

1. 准确度降低，经常非全局最优

2. 不易于并行实现

样本量比较大，或者在线学习算法

小批量梯度下降 MBGD

损失函数使用一部分样本

综合BGD、SGD

一般情况

传统普通梯度下降

或：批量梯度下降（Batch Gradient Descent，BGD）

根据李航《统计学习方法》改编

梯度下降为最优化算法，顾名思义，优化，需要迭代才能找出最优值。

这里 $\theta$ 未知，所以梯度下降整个过程其实就是求 $\theta$ ！！求出来还是个估计值！

输入：损失函数 $J(\theta)$ ， $\theta$ 为向量， $\theta = (\theta_0,\theta_1,\theta_2,...,\theta_n )$ ，n个特征

输出： $\theta$ 的最优值，用 $\theta^{*}$ 表示， $\small \theta^{*} = (\theta_0^{*},\theta_1^{*},\theta_2^{*},...,\theta_n^{*} )$

设损失函数为 $J(\theta)$

说明： $J(\theta)$ 一般为平方损失、log对数损失等 能求导的 损失函数，0-1损失等不能求导则不能用梯度下降

（图片）

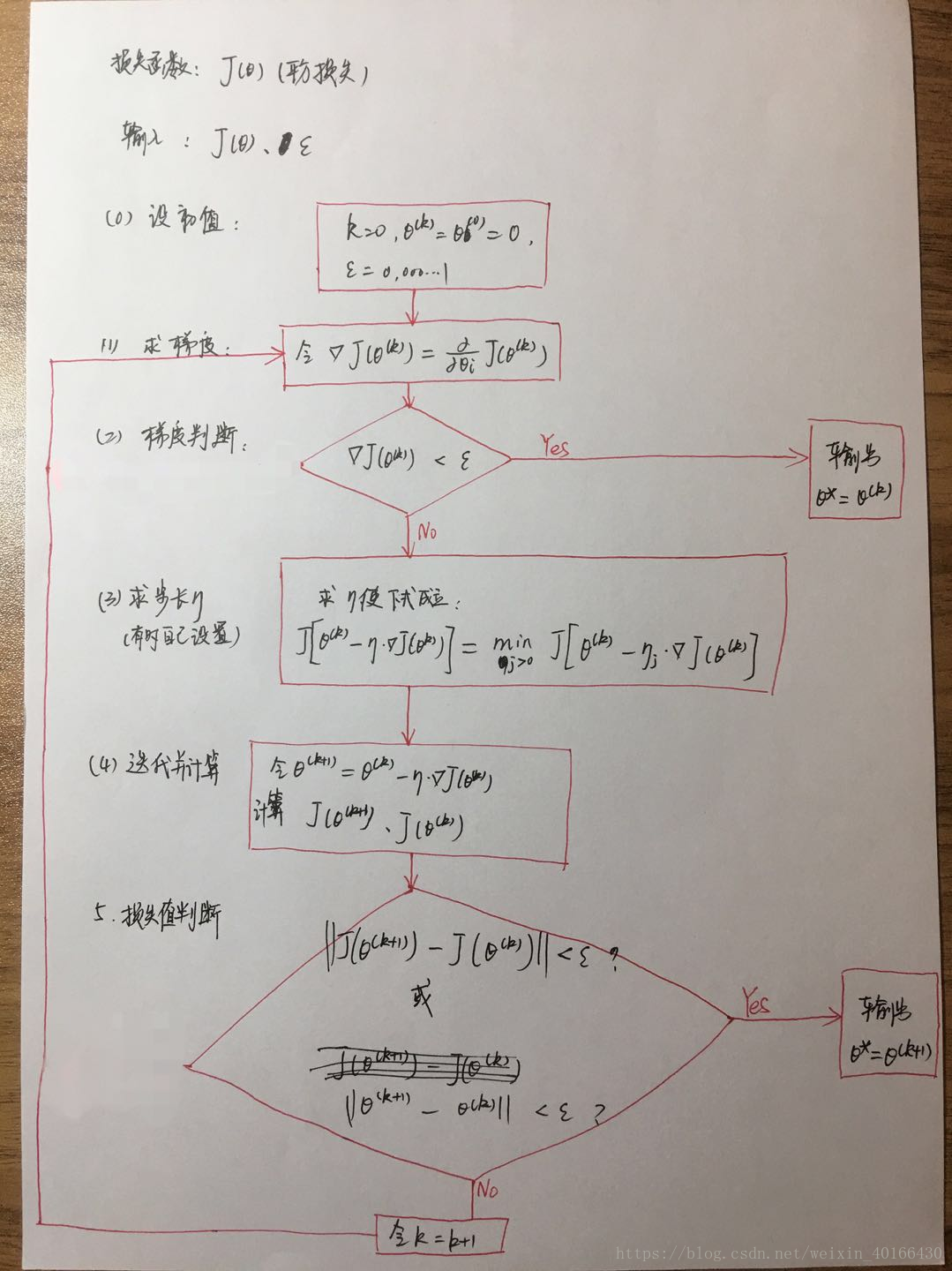
说明：

1. k=0，是为了方便，有需要可以输出迭代次数，这样可以比较不同优化算法中的速率。

2. $\small \theta^{(k)}=\theta^{(0)}=0$ 也是自己为了方便设置的，当然也可以设别的初值，或者设置不同初值重复多次试验，对比最优值结果。不同初值可能会得出不同的优化结果，这是由于进入的局部最优值的情况，但是！如果损失函数为凸函数，那么最优值只有一个！只有一个！可以放心设置初值，只是时间不同而已，多迭代几次便是了。

3. $\small \epsilon$ 是一个大于0，但非常接近0的一个数，比如0.000001，用来做最后的参考，比如两个函数值的差值小于 $\small \epsilon$ ，那么就可以判定两个函数值相等，那么基本收敛了，数学分析的收敛知识点就这玩意儿。当然根据实际需求， $\small \epsilon = 0.01,\epsilon = 0.1$ ，也是可以的。