grey code 格雷码

题目描述

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

For example, given n = 2, return[0,1,3,2]. Its gray code sequence is:

00 - 0
01 - 1
11 - 3
10 - 2

Note:
For a given n, a gray code sequence is not uniquely defined.

For example,[0,2,3,1]is also a valid gray code sequence according to the above definition.

For now, the judge is able to judge based on one instance of gray code sequence. Sorry about that. 

格雷码的产生方法一：                            

以二进制为0值的格雷码为第零项，第一项改变最右边的位元，第二项改变右起第一个为1的位元的左边位元，第三、四项方法同第一、二项，如此反复，即可排列出n个位元的格雷码。

假设原始的值从0开始，格雷码产生的规律是：

第一步，改变最右边的位元值；

第二步，改变右起第一个为1的位元的左边位元；

第三步，第四步重复第一步和第二步，直到所有的格雷码产生完毕（换句话说，已经走了(2^n) - 1 步）。

用一个例子来说明：

　　假设产生3位元的格雷码，原始值位 000

　　第一步：改变最右边的位元值： 001

　　第二步：改变右起第一个为1的位元的左边位元： 011

　　第三步：改变最右边的位元值： 010

　　第四步：改变右起第一个为1的位元的左边位元： 110

　　第五步：改变最右边的位元值： 111

　　第六步：改变右起第一个为1的位元的左边位元： 101

　　第七步：改变最右边的位元值： 100

解析 1: 映射法

思路：我们通过对格雷码进行观察，发现格雷码具有映射关系。n位元的格雷码可以从n-1位元的格雷码以上下镜射后(一半顺序，一半逆序再加1<<n)加上新位元的方式快速的得到。我们从一个比特位的格雷码开始计算，直到得到N个比特位的格雷码。第一位是 0 + 1<<0, 0 + 1<<1.

实现代码：

             class Solution {
public:
    vector<int> grayCode(int n) {
         vector<int> ret{0};  
        for(int i = 0; i < n; i++)  
        {  
            int curCnt = ret.size();  
            //把当前数字按照逆序顺序添加到ret中  
            while(curCnt)  
            {  
                curCnt--;  
                int curNum = ret[curCnt];  
                curNum += (1 << i);  
                ret.push_back(curNum);  
            }  
        }  
        return ret;  
    }

};

解析2：

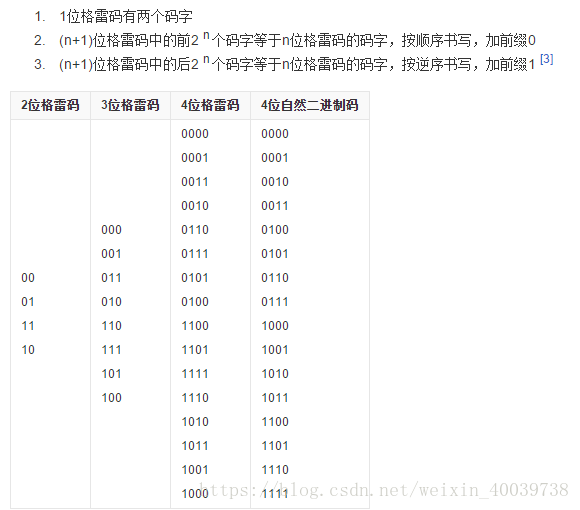
解法2不过是返回的是字符串类型

               

if(n==1)
    {
        vector<string> v;
        v.push_back("0");
        v.push_back("1");
        return v;
    }
    else
    {
        vector<string> v;
        vector<string> v1;
        v1=gray_code(n-1);
        
        for(int i=0;i<v1.size();i++)
        {
            v.push_back("0"+v1[i]);
        }
        for(int i=(v1.size()-1);i>-1;i--)
        {
            v.push_back("1"+v1[i]);
        }
        
        return v;