最优化方法
1 优化目标的函数
1.1 无约束优化

1.2 约束优化


1.3 等式约束

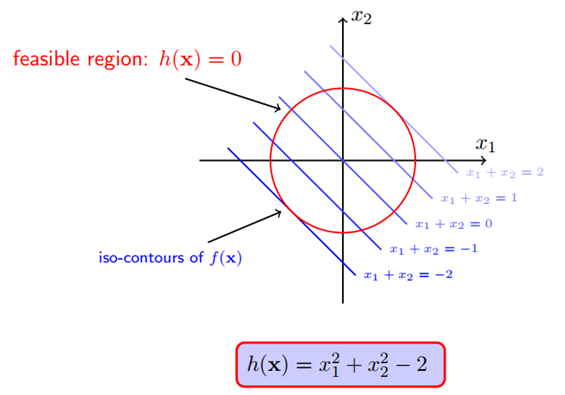

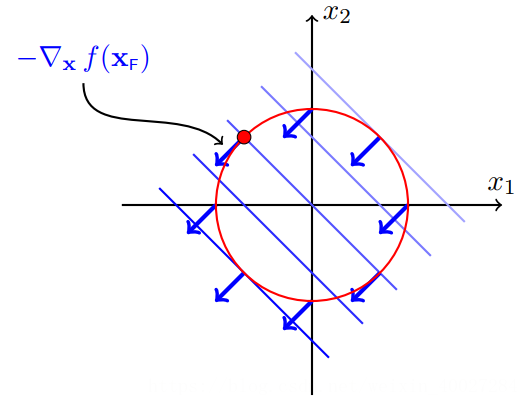
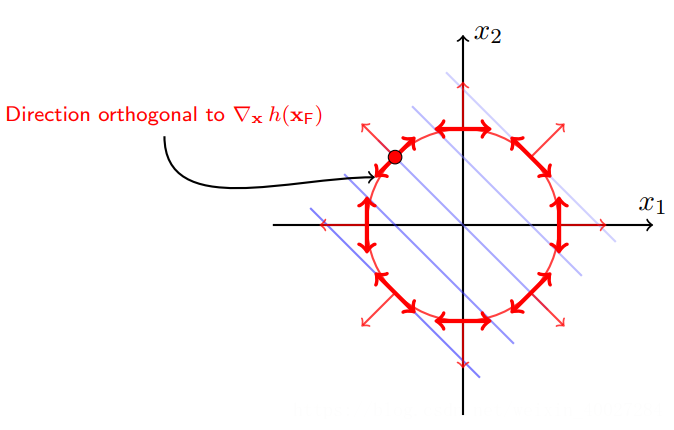
容易发现,在关键的极小值点处,f(x)的负梯度和h(x)的梯度在同一直线上,如下图左下方critical point的蓝色和红色箭头所示。
注意图中所示是同向的,但是这里并不一定是同向,有可能反向(因为等式约束h(x)=0,把h(x)变成-h(x)求解是一样的,这个时候h(x)的梯度就相反了)
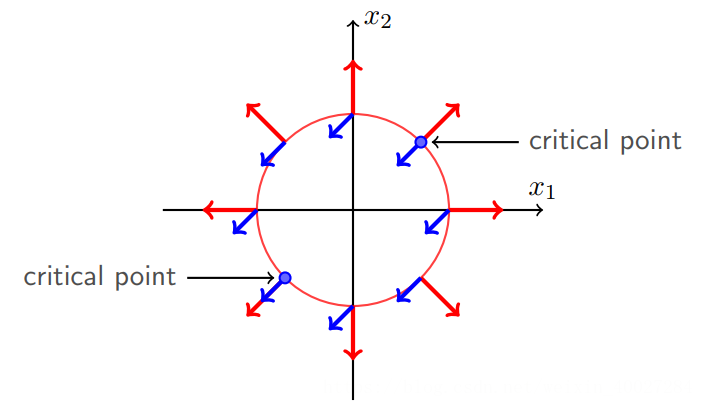
由此可知,在极小值点,h(x)和f(x)的梯度在同一线上,有
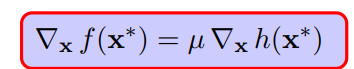

 特别注意:优化问题是凸优化的话,通过上图两个条件求得的解就是极小值点(而且是全局极小)。不是凸优化的话,这两个条件只是极小值点的必要条件,还需要附加多一个正定的条件才能变成充要条件,如下图所示(半正定得到的是极小,正定得到的是严格极小)。
特别注意:优化问题是凸优化的话,通过上图两个条件求得的解就是极小值点(而且是全局极小)。不是凸优化的话,这两个条件只是极小值点的必要条件,还需要附加多一个正定的条件才能变成充要条件,如下图所示(半正定得到的是极小,正定得到的是严格极小)。

1.4 不等式约束
对于不等式约束g(x)<=0,和等式约束h(x)=0不一样,h(x)=0可以在平面上画出一条等高线,而g(x)<=0是一个区域,很多个等高线堆叠而成的一块区域,我们把这块区域称为可行域。
不等式约束分两种情况来讨论,第一种是(不考虑可行域限制时的)极小值点落在可行域内(不包含边界),第二种是(不考虑可行域限制时的)极小值点落在可行域外(包含边界)。
下面举两个例子来解释这两种情况,然后总结两种情况给出转换求解。
1.4.1 极小值点落在可行域内(不包含边界)

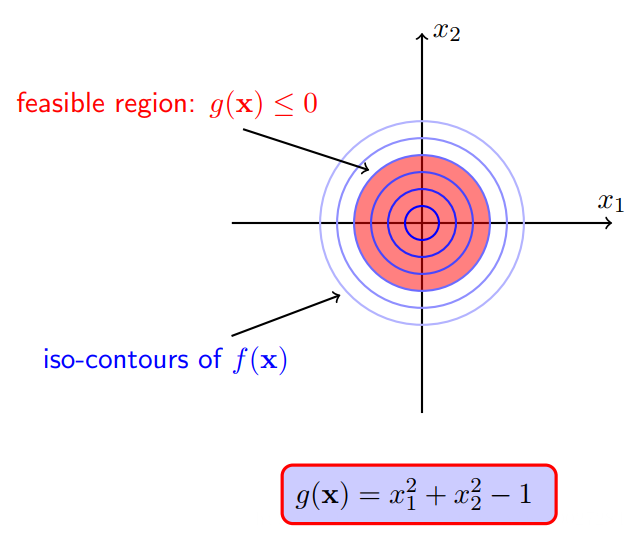
1.4.2 极小值点落在可行域外(包含边界)

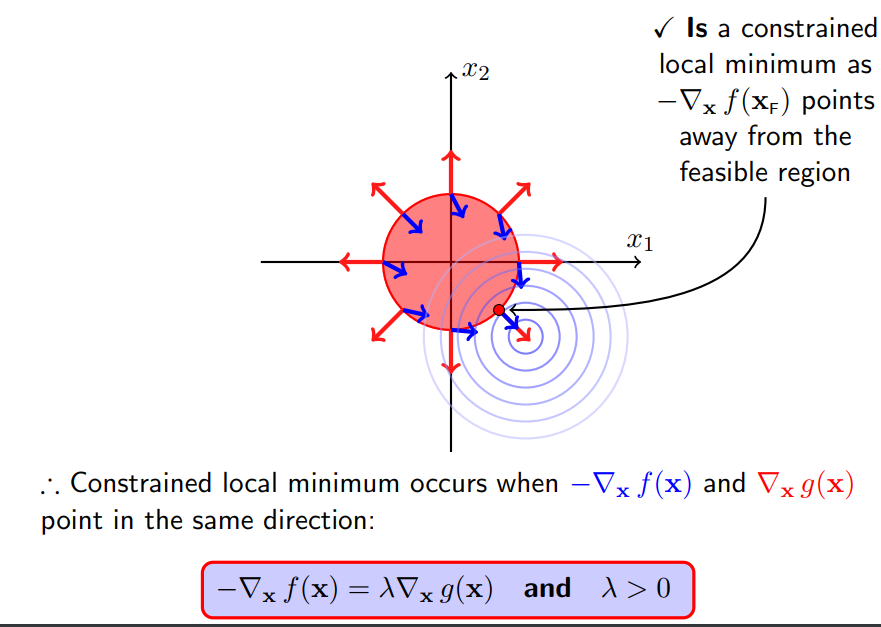
1.4.3 总结
极小值点落在可行域内(不包含边界):这个时候可行域的限制不起作用,相当于没有约束,直接f(x)的梯度等于0求解,这个时候g(x极小值点)<0(因为落在可行域内)。
极小值点落在可行域外(包含边界):可行域的限制起作用,极小值点应该落在可行域边界上即g(x)=0,类似于等值约束,此时有g(x)的梯度和f(x)的负梯度同向。
 总结以上两种情况,可以构造拉格朗日函数来转换求解问题。对于不等式约束的优化,需要满足三个条件,满足这三个条件的解x*就是极小值点。这三个条件就是著名的KKT条件,它整合了上面两种情况的条件。
总结以上两种情况,可以构造拉格朗日函数来转换求解问题。对于不等式约束的优化,需要满足三个条件,满足这三个条件的解x*就是极小值点。这三个条件就是著名的KKT条件,它整合了上面两种情况的条件。
特别注意:优化问题是凸优化的话,KKT条件就是极小值点(而且是全局极小)存在的充要条件。不是凸优化的话,KKT条件只是极小值点的必要条件,不是充分条件,KKT点是鞍点,是可能的极值点。也就是说,就算求得的满足KKT条件的点,也不一定是极小值点,只是说极小值点一定满足KKT条件。
 不是凸优化的话,还需要附加多一个正定的条件才能变成充要条件,如下图所示(半正定得到的是极小,正定得到的是严格极小)。
不是凸优化的话,还需要附加多一个正定的条件才能变成充要条件,如下图所示(半正定得到的是极小,正定得到的是严格极小)。

1.5 优化问题总结
拓展一下,对于同时有多个等式约束和多个不等式约束,构造的拉格朗日函数就是在目标函数后面把这些约束相应的加起来,KKT条件也是如此,如下图所示。

考虑凸优化问题:
对于无约束的优化问题,直接令梯度等于0求解。
对于含有等式约束的优化问题,拉格朗日乘子法,构造拉格朗日函数,令偏导为0求解。
对于含有不等式约束的优化问题,同样构造拉格朗日函数,利用KKT条件求解。
2. 最优解求解方法
2.1 需要求导的方法
目标函数知道以后,可以采用最小二乘法,梯度下降,牛顿法,拟牛顿法等来求解。梯度下降法我们都很清楚了,下面介绍一下牛顿法:
2.1.1 牛顿法
牛顿拉夫森迭代法求解方程f(x)=0:

2.2 不需要求导的方法
但是当方程无法求导的时候(lasso回归)上述方法都失效了。可以采用下面的方法
2.2.1 坐标轴下降法


2.2.2 前向梯度算法


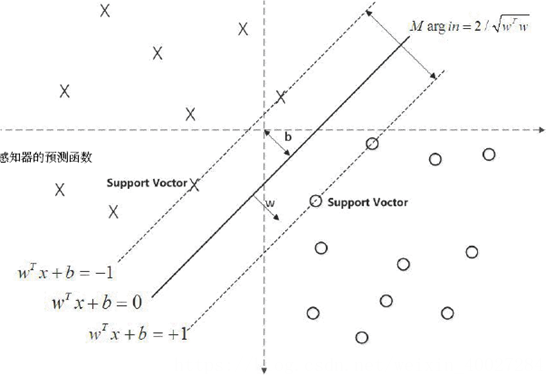
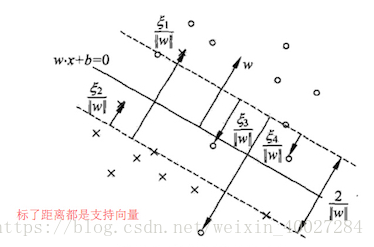
附录 函数距离

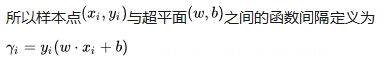



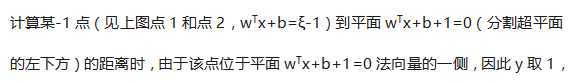
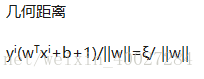
























 5170
5170

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








