python训练的准确率保持在低水平不变的原因_机器学习中的测试准确率很低的原因竟然是这样，我要曝光它...

背景

曾经，在图片识别领域，关于机器学习在训练和测试的时候会出现准确率不是很高的问题，我问过一位大学教授，以下我们的对话：

我：我们搞机器学习时遇到训练和测试的准确率不是很高，是什么原因？

教授：我们的模型有些地方没学习到，样本量太少了。

我：那多少个样本才合适呢？

教授：问题不是样本量有多少，而是让模型把每一个地方都学到，这样识别率才会提上去。

常见的两个现象

我相信做过机器学习的人都应该遇到两个现象

一、刚开始的时候，我们模型的准确率不会是很高，可以通过一些办法可以做进一步的改进。

为了提升准确率会做以下几方面的工作：

1.调整参数

2.增加样本量

3.拓宽模型节点数，或者加深网络层数

4.尝试新的模型

4种办法是我们常用的，具体要增加多少个节点、多少层网络才合适呢？都是一步一步去尝试，比较才知道要定多少是合适的。

二、训练的时候准确率很高，而到了测试的时候准确率就很低，为什么？

网上搜了一下这个问题的答案，解析都是模型过拟合，解决办法是重新打乱训练数据和测试数据，或者增加样本量，或其他一些办法。

放大招

至于第二点中给出的解决办法，大家都公认是正确的，我也觉得没问题，但是，但是，我觉得解析还不够透彻，我是这么理解的：

不管是打乱原始数据再分成训练数据，还是增加样本数量，目的都是使得训练数据的特征保持和测试数据的特征是一样的，这样才能使得测试的时候的准确率跟训练的时候接近。

举个例子:假设训练数据我们已经知道有n个特征，表示为x=(x1,x2,x3,...,xn),也已经训练好了模型y=f(x)，测试数据的特征假设为xx=(xx1,xx2,xx3,...,xxn),当我们把测试数据直接代入模型，误差也许会很小，也可能会很大，原因如下：1. 误差很小：x==xx 训练数据和测试数据等价，从数学角度理解是x经过恒等变换后变成xx，即x=g(xx) [恒等变换公式E(x)=x]2. 误差很大：x!=xx x 和 xx相差很大，不能经过恒等变换达到x=g(xx)，预测的准确度低是必然的。

如果x!=xx，又想让测试误差变小有没有办法呢，答案是有的。

答案其实不难，我们只要在x和xx之间建立好一个恰当的函数关系x=S(xx)，建立复合函数y=f[S(xx)],这样我们就可以提高测试的准确率了。

案例解析

在工厂中，我们会使用铣刀去切割材料，每次切割时会用传感器接收X轴、Y轴、Z轴的压力信号、声音信号等一些数据，以及切割前后刀具的磨损数据，然后建立模型来预测刀具的使用寿命。

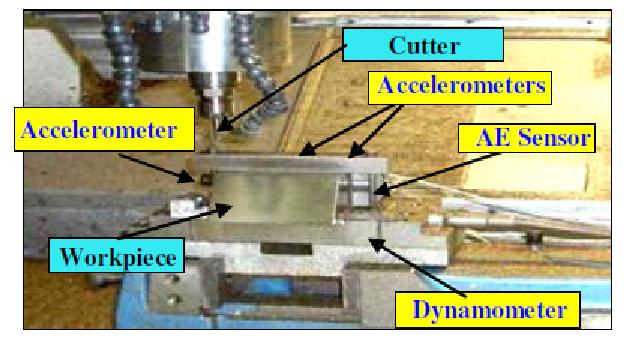
作业背景

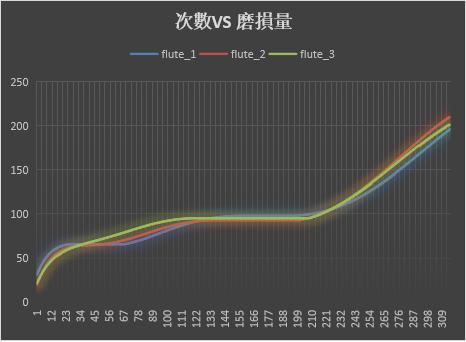
一把刀有3个刀刃，横轴是使用次数，纵轴是磨损程度

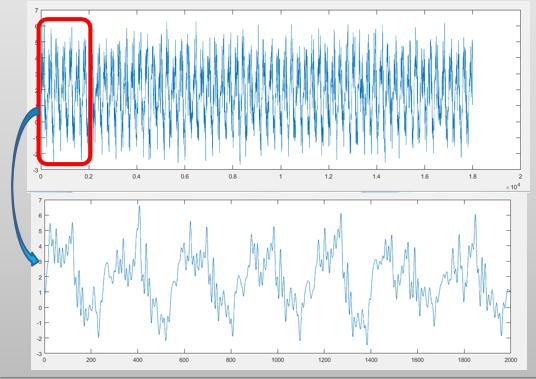
每次切割时采集到的X方向的震动数据及局部放大

由于每次切割的时长为十几分钟，数据采集频率为1000笔/秒，一次切割生成一个文件，一个文件夹下会包含一把刀从开始使用到淘汰的所有数据，一般是300+笔。

刀具A分别在X、Y、Z方向上进行FFT变换的图像，001表示第一次使用，180表示第180次使用

从上图右侧可知，在固定频率上有信号增长，把一个文件夹的所有文件经过FFT变换后，即可提取到他们的特征。

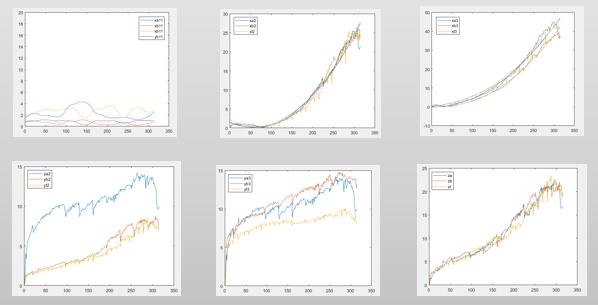
刀具A和刀具B在固定频率下的特征

至此，我们已经提取到自变量X，也已经知道因变量y,就可以建立他们的函数关系

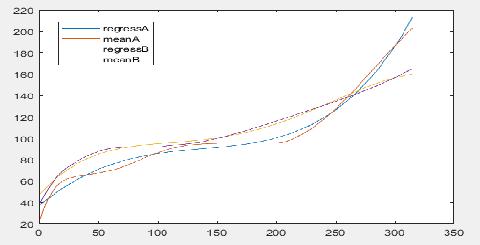
meanA表示实际的平均，regress表示提取特征后建立的函数关系

从上图可以看出，建模的效果还是不错的，用刀具A和刀具B做相互测试结果会是怎么样呢？

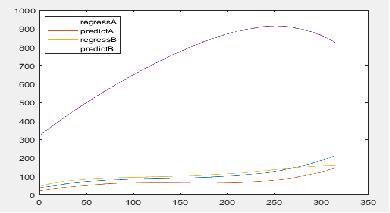
相互预测

很显然，相互预测的结果并不理想。如果使用前面所讲的办法建立自变量之间的关系后，效果会不会好呢？

很明显，自变量是二次曲线，我们建立一个自变量之间的二次函数

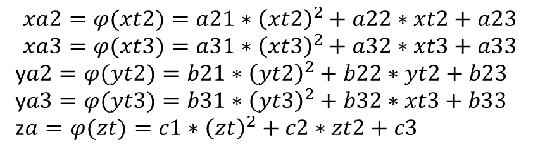
自变量变换

把上述关系导入磨损函数

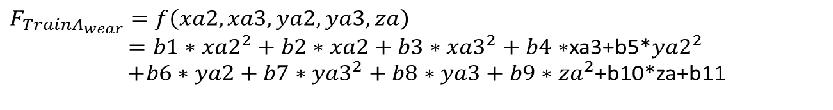
原始磨损函数

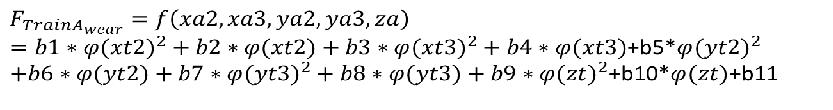
磨损复合函数

把刀具A和刀具B同时用来预测Test这把刀，准确度有较大提高。

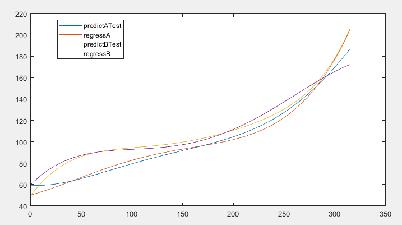
刀刃1 刀具A和刀具B同时用来预测Test这把刀

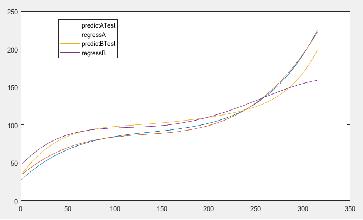
刀刃2 刀具A和刀具B同时用来预测Test这把刀

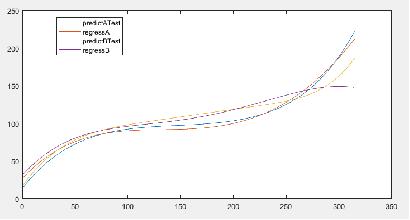
刀刃3 刀具A和刀具B同时用来预测Test这把刀

结论

在本文章中，我用解析函数的方式解析机器学习的原理，也讲解了预测效果不理想的原因，但是本办法由局限性，即本办法仅对于我们能提取全部特征的数据是有效的，而有时候我们不知道哪些特征是有效的哪些是无效的，或有时候特征的数量会很多，达到几千甚至几万的时候，要建立解析函数是不可能的，也许要先经过PCA降维。本文仅作为参考，要想得到更理想的结论，需深入研究，探索更科学合理的办法。