群同态基本定理证明_专栏简介与群表示论

【Meet in Maths：由于现代数学的发展过于庞杂，本专栏在力图严谨、清晰、简洁的框架下，分享一些整理的数学笔记的心得，做一些抛砖引玉的活~（本专栏要求具备本科数学系的基础知识以及大学物理的基础知识）当然，我们最终的目标是尝试在基础数学的主要分支上做到一些前沿性的整理：代数（代数几何）；几何（低维拓扑）；分析（偏微分方程）；概率（无穷维随机分析 & 随机微分几何）。如果笔者还有能力，可能会再考虑理论物理上的一些记录。当然，一切只是一个“极大理想”。】

---

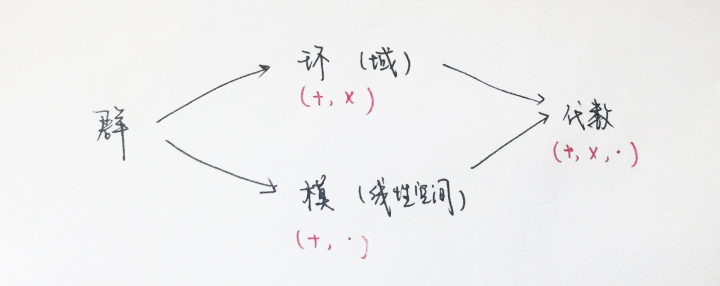
群论（Group Theory）是现代数学尤其是代数学分支很重要的一个领域，并且也为现代数学提供了一种最基础的语言，研究群的目的是为了研究这个群的具体结构。

首先，我们先抽象的了解一下什么是群以及群是怎么来的？

一个群（Group）是一个比较好的代数系统，一般的定义是：如果一个集合上有一个二元（封闭的）运算（本质是一个映射），且满足有单位元e、结合律以及可逆性，那么这个集合称为一个群。

例如整数集Z，取加法为定义中的二元运算，即把Z中的任意两个元素a、b映射到a+b还是属于Z，并且0是单位元，a的逆显然是-a，加法运算保证了结合律。再例如n维矩阵构成的集合在乘法运算下也构成一个群。

数学中有很多这样的在上述性质的二元运算下的集合，我们把这种特性抽象提取出来，于是有了群的概念。

现代数学研究群的结构一般有两种方法，并且这两种方法对应了两门不同的研究群的课程（前者是后者的基础）：

• 第一种方法：研究它的子群

“To study a group, it is important to study its subgroups!”

第一步：导出正规子群与商群的概念

【子群】什么是一个群G的子群（Subgroup）？G中的子集H如果还是一个群（即在原来群的运算下封闭），那么我们称H为G的子群，记作H≤G。

【陪集】给定一个群G，我们先看看它的阶数（元素的个数）与它子群阶数的关系，这就引申出了子群H的陪集（Coset）的概念：对于H≤G，H的陪集可以看做群G关于H的一个划分，并且划分下每个等价类称为子群H在G中的陪集。类似于陪跑的概念，把鲍勃·迪伦及他的粉丝看成文学者构成集合的“子群”，那么陪跑的村上春树及他的粉丝就是鲍勃的一个“陪集”。并且所有等价类中的元素的势（Cardinality） 相等（即可以建立一一对应关系），于是进一步有了拉格朗日定理：说明了有限群的子群的阶数（所有元素的个数）一定整除G的阶数。这个性质可以大大提高我们对G的子群的了解，例如素数阶群一定是循环群等等。

【正规子群与商群】但是光利用陪集将G进行划分还不够，我们想找个性质更好一点的子群N，使N的所有陪集构成一个群（每个陪集即等价类看成一个元素），即商群（Quotient Group），记为G/N。通过运算我们知道必须让N是G的正规子群（Normal Subgroup），即在G的共轭作用下不动，记为N⊴G（即每个元素去干扰这个集合，但这个集合依然不变，有点出淤泥而不染的感觉）。更进一步地，我们又可以得到关于商群的群同态三个基本定理等等。（注：同态是两个群之间的一个映射，这个映射保证了两个群关于运算的相似性，而若这个映射是双射，那么称这两个群同构，即两个群“一模一样”）

第二步：深入研究正规子群和商群

【单群】既然有了正规子群的概念，研究到这里就足够了吗？显然还不够，因为只用定义去找正规子群是很！困！难！的！我们首先想知道G有没有非平凡的正规子群？如果有那么有多少个？一个性质是如果G没有非平凡的正规子群，即G只有{e}和G本身是G的正规子群，则称G是一个单群（Simple Group）。

【正规子群序列】那么如果G不是单群，即至少有一个非平凡的正规子群，可不可以考虑G的正规子群、G的正规子群的正规子群、G的......？这样就形成了一个正规子群序列（Normal Subgroup Sequence），也就是{e}=Gn⊴...⊴G2⊴G1⊴G0=G，Gi+1是Gi的正规子群。（注意，Gi+2不一定是Gi的正规子群！）

【合成序列】如果G有这个正规子群序列，那么我们可不可以再进行分解，即每两个中间再插一些，分成原来基础上更细的序列，直到不能更细（也就是Gi/Gi+1为单群，且Gi≠Gi+1）？合成序列的定理告诉我们，对于有限群G来说答案是肯定的，也就是G的任意一个正规子群序列可以加细成为合成序列（Composition Sequence），不能再加细，类比于24的因子的一个序列（1，4，24）可以加细成（1，2，4，8，24）。（任意相邻两数的商是素数）

【Jordan-Holder定理】那么问题又来了，24可以有（1，2，4，8，24）这个因子序列，也可以有（1，2，4，12，24）这个因子序列，（1，4，24）分到最后的两个因子序列的长度是不是一样，相邻两个元素的商可不可以有个一一对应？也就是G的两个合成序列{e}=Gn⊴...⊴G2⊴G1⊴G0=G与{e}=Hm⊴...⊴H2⊴H1⊴H0=G中的m是否等于n？以及{Gi/Gi+1}与{Hi/Hi+1}见是否有个一一对应？Jordan-Holder定理告诉我们答案是肯定的。

【有限单群分类定理】至于合成序列与单群为什么这么重要，是因为在深入研究一个有限群G时，经常会发现一个命题对有限群G成立当且仅当对它合成序列中的有限单群Gi/Gi+1也成立！进而会很多数学家对有限单群进行深入研究。而有限单群分类定理是对单群进行分类研究这项巨大工程的重要产物，但由于单群分类定理的证明非常不漂亮，用了长达五千多页的文字，并且证明存在漏洞还没有完全修补完！所以暂时还不为大多数数学家所接受，因此目前也有很多人试图用更简洁的证明来将有限单群进行分类。在此我们就不深入讨论下去了。

【可解群】好了，我们再回到正规子群序列，另一个角度看它的性质（注意：不一定是合成序列）。存不存在某一个正规子群序列使得Gi/Gi+1是一个Abel群（即运算可以交换的群，又称交换群）？如果存在，我们称G为一个可解群（Sovable Group）。一个显然的命题是一个单群如果不是Abel群，那么它不可解，所以由一些定理可以知道，n≥5时，由于An是单群但非Abel群所以导致An是不可解的，所以Sn是不可解的。

【换位子群】但是找一个性质这么好的序列来判定G为可解群太过麻烦，我们换一种思路：反推一下，如果N是G的正规子群，那么G/N是Abel群有没有什么等价定义？通过反演推算我们可以得到G的子群换位子群G'（Commutator Subgroup）这么一个概念，（G'还是G的正规子群）并且可以知道G/N为Abel群等价于N是G'的子群，即G'是N的一个支撑，这样可以得到有限群G为可解群的另一种等价定义：G可解等价于G的换位子群序列Gn⊴...⊴G2⊴G1⊴G0=G（即Gi+1是Gi的换位子群）能下降到{e}，即存在n使得Gn={e}。这样大大方便了我们研究G是否可解的充要条件。

到此，《抽象代数》中研究群的子群这个主干线就告一段落。

---

• 第二种方法：群表示

注：1. 以下，

，

，由于有限群的不可约

表示都是有限维，因此

，即表示皆“有限”；2. 本文中同一个表示皆指等价的表示组成的等价类，不同的表示皆指不等价的表示。

• 什么是表示？什么是群的表示？

表示理论（Representation Theory）是代数学的一个重要的方向，现代的表示论除了研究有限群的表示，还研究结合代数的表示、李代数的表示，甚至抽象到模表示等等。

群的表示也就是研究给定的群

到另一个群

的保持运算的映射（即同态），通过同态映射，我们通过了解我们熟悉的

的性质来认识原来的群

的结构，即把未知的事物与一个熟悉的事物联系起来，通过这种联系来认识原来未知的事物，这种研究方法也是现代数学一个鲜明的特色。而本文只研究第一部分——有限群的表示。

• 表示与作用的等价

用数学的语言来说，即先考虑群

在集合

上的

作用（Action）:

满足：1.

，

；2.

：

,

。

如果把

简记为

，则有更简洁的定义：1.

；2.

。其中这个定义诱导了一个同态映射

，其中

是

的全变换群（

到

的所有双射构成的群），而这个同态又称为群

的一个

表示（Representation）。

反过来，一个表示（即同态映射

）也可以诱导一个群作用。

所以，表示和作用