pv原语模拟实现_用EXCEL和Python分别模拟蒙特卡洛模型

大数据时代，数据就是生产力。掌握数据处理、分析方法非常必要。本篇针对一个模拟蒙特卡洛模型的案例，介绍如何用EXCEL和Python两种工具分别实现。希望从“道”和“术”两方面给读者一些启迪。

什么是蒙特卡洛模型

蒙特卡罗模型是一种随机模拟方法。以概率和统计理论方法为基础的一种计算方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名。(来源于百度百科)

投资回报模型

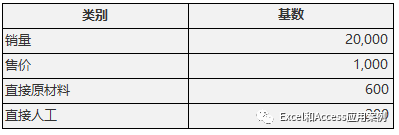
我们使用一个简化的投资回报模型：某公司为迎合市场需要，准备研发并生产新产品，前期需要投入不菲的研发费用和设备成本。对于初始投资、销量、售价、变动成本(直接原材料、人工)均存在不确定性，但可以根据可能金额估计发生概率。如下表：

不确定性假设：

基数：

净现值(NPV)的计算公式

前提假设：

1、假设此业务每年产生的现金流等于此业务的利润，即不考虑应收、应付等因素带来的影响。

2、假设此业务每年产生的现金流相同，即，计算年金现值。

3、回报期考虑5年，贴现率(最低报酬率)为12%。

4、不考虑税费影响。

NPV=PV(12%，5，每年净现金流)-投资支出

基于EXCEL的投资回报模型模板

思路：

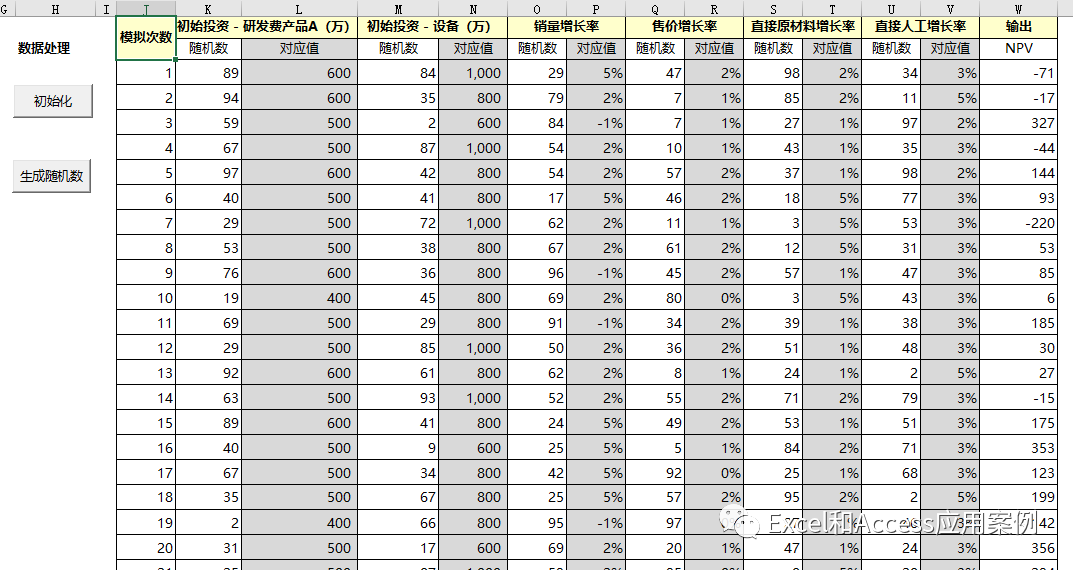
1、使每一个变量对应一个随机数，随机数的范围是0~99之间的整数。根据随机数的范围对应“发生概率”，比如如果随机数落在0~19之间，那么概率为20%。

2、使用VBA来生成随机数，避免将随机数直接作为值放在单元格，影响表格计算速度。

3、用LOOKUP函数根据随机数值，找到对应的概率。

数理统计基础

大数据分析本质上还是用到了基本的数理统计方法：

1、平均数：(不解释)

2、标准差(Standard Deviation) ，中文环境中又常称均方差，是离均差平方的算术平均数的平方根，用σ表示。在概率统计中最常使用作为统计分布程度上的测量。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。(来源于百度百科)

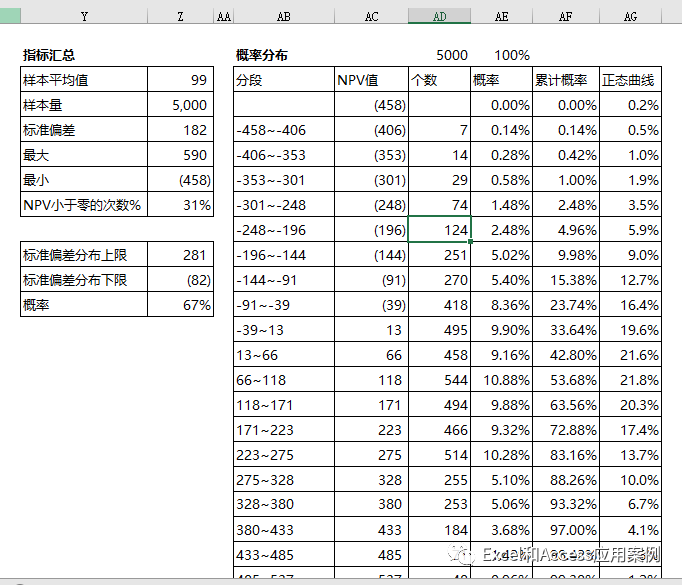
股票分析中也经常用到这些方法。我们这个案例通过多次模拟(5000次)，得到不同的结果，计算结果的平均值和标准差，体现风险的大小。

计算统计结果

思路：不需要考虑详细的公式，使用EXCEL的stdev公式就可以直接计算出标准差。

指标解释：NPV值落在-82~+281区间的概率为67%，小于零的概率为31%(NPV<0代表不应该投资此项目)。

绘制概率直方图和正太分布曲线

思路：

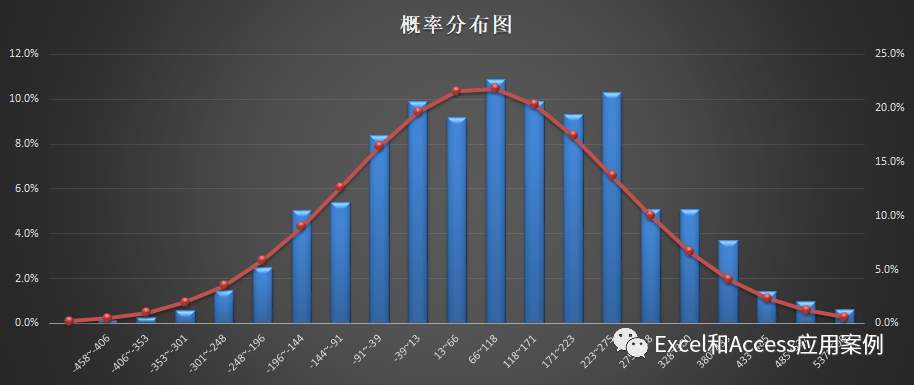
1、将NPV出现的范围区间尽可能缩小(本例自动分为20个区间)，使用COUNTIF公式计算出现次数，即算出概率。 

2、用EXCEL直方图和模拟曲线绘制相应图形。

未完待续

篇幅所限，用Python进行模拟的思路和方法将在下篇介绍！