地理坐标与投影坐标解析-优快云博客

一.引言

地理信息系统（Geographic Information System或 Geo－Information system，GIS）有时又称为“地学信息系统”。简称GIS，它是一种特定的十分重要的空间信息系统。它是在计算机硬、软件系统支持下，对整个或部分地球表层（包括大气层）空间中的有关地理分布数据进行采集、储存、管理、运算、分析、显示和描述的技术系统。与遥感技术（Remote sensing，RS)、全球定位系（Global positioning systems，GPS）统称为“3S技术”。在常用的GIS软件（如ArcGIS）中，经常会接触到投影坐标和地理坐标以及垂直坐标，本篇博文对地理坐标和投影坐标进行简单的总结。由于本人水平有限，文中出现不当或错误之处请及时与我取得联系，第一时间进行纠正，方便大家彼此学习，共同进步。

二.基本概念

地理坐标系：为球面坐标。就是用经纬度来表示地面点位的球面坐标。参考平面地是椭球面，坐标单位：经纬度；

大地经度：参考椭球面上某点的大地子午面与本初子午面间的两面角。东正西负。

大地纬度 ：参考椭球面上某点的法线与赤道平面的夹角。北正南负。

大地高：指某点沿法线方向到参考椭球面的距离

投影坐标系：为平面坐标。参考平面地是水平面，坐标单位：米、千米等；
地理坐标转换到投影坐标的过程可理解为投影。（投影：将不规则的地球曲面转换为平面，二维到三维）

三.地理坐标系

3.1大地水准面

地球的自然表面有高山也有洼地，是崎岖不平的，我们要使用数学法则来描述他，就必须找到一个相对规则的数学面。

大地水准面是地球表面的第一级逼近。假设当海水处于完全静止时的平衡状态，从海平面延伸到所有大陆下部，而与地球重力方向处处正交的一个连续、闭合的曲面，这就是大地水准面。

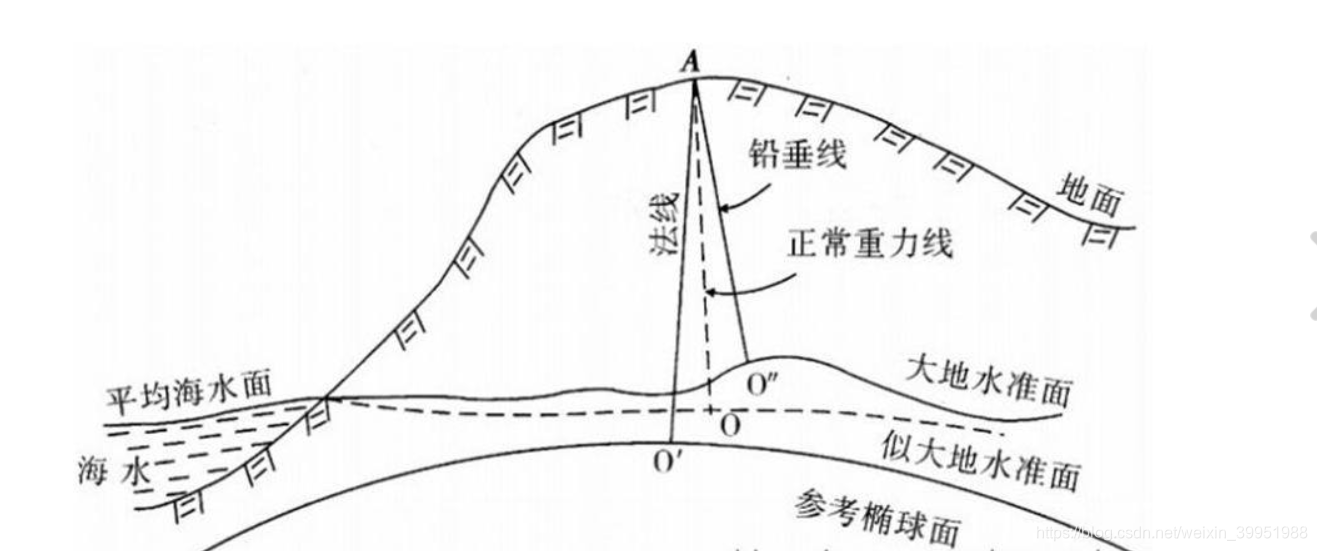
3.2 地球椭球体

大地水准面可以近似成一个规则成椭球体，但并不是完全规则，其形状接近一个扁率极小的椭圆绕短轴旋转所形成的规则椭球体，这个椭球体称为地球椭球体。它是地球的第二级逼近。

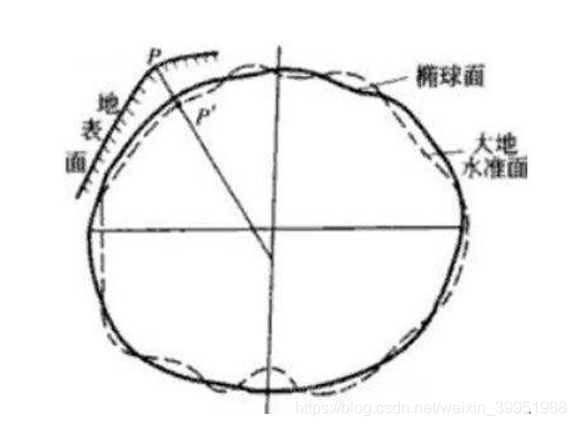
3.3 大地基准面

确定了一个规则的椭球表面以后，我们会发现还有一个问题，参考椭球体是对地球的抽象，因此其并不能去地球表面完全重合，在设置参考椭球体的时候必然会出现有的地方贴近的好（参考椭球体与地球表面位置接近），有地地方贴近的不好的问题，因此这里还需要一个大地基准面来控制参考椭球和地球的相对位置。这是地球表面的第三级逼近。有以下两类基准面：

地心基准面：由卫星数据得到，使用地球的质心作为原点，使用最广泛的是 WGS 1984。

区域基准面：特定区域内与地球表面吻合，大地原点是参考椭球与大地水准面相切的点，例如Beijing54、Xian80。我们通常称谓的Beijing54、Xian80坐标系实际上指的是我国的两个大地基准面。

我们通常说的参心大地坐标系和地心大地坐标系的区别就在于此。
参心大地坐标系：指经过定位与定向后，地球椭球的中心不与地球质心重合而是接近地球质心。区域性大地坐标系。是我国基本测图和常规大地测量的基础。如Beijing54、Xian80。
地心大地坐标系：指经过定位与定向后，地球椭球的中心与地球质心重合。如CGCS2000、WGS84。

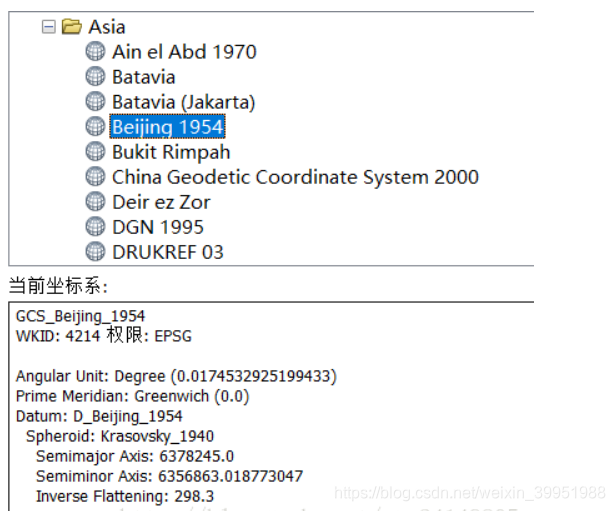
下图为ArcGIS中北京1954地理坐标系的参数信息：

四.投影坐标系

在ArcGIS 中选择投影坐标系的首时候，会出现如下图所示的一大堆北京1954坐标系，

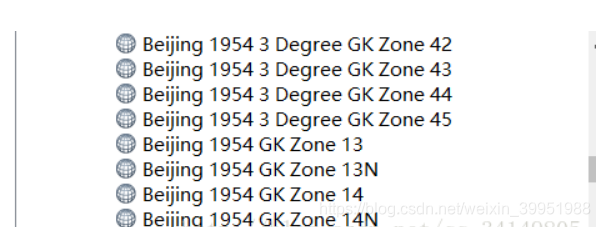
首先，投影坐标系的生成是以地理坐标系为基准的，所以每个投影坐标系前面都会挂有地理坐标系。而地理坐标系后面的则是投影参数，

比如 Beijing 1954 3 Degree GK Zone 42

意思是：3度分带法的北京54坐标系，中央经线在东126度的分带坐标，横坐标前加带号。

4.1 投影

在地球椭球面和平面之间建立点与点之间函数关系的数学方法，称为地图投影。

地球椭球表面是一种不可能展开的曲面，要把这样一个曲面表现到平面上，就会发生裂隙或褶皱。在投影面上，可运用经纬线的“拉伸”或“压缩”（通过数学手段）来加以避免，以便形成一幅完整的地图。但不可避免会产生变形。
地图投影的变形通常有：长度变形、面积变形和角度变形。在实际应用中，根据使用地图的目的，限定某种变形。

4.2 投影带的计算

我们经常会听到6°分带，3°分带的说法。其实并不是所有投影都有分带，从下面一张图就可以看出，分带是高斯克吕格投影自带的。

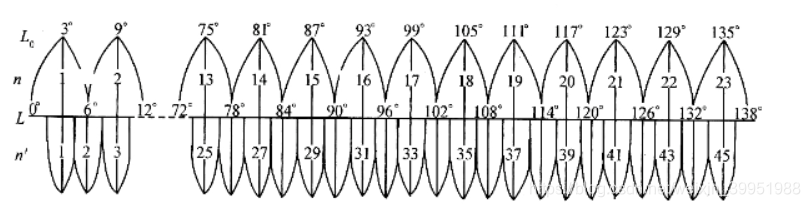
高斯－克吕格投影分带规定：该投影是国家基本比例尺地形图的数学基础，为控制变形，采用分带投影的方法，在比例尺1：2.5万—1：50万图上采用6°分带，对比例尺为1：1万及大于1：1万的图采用3°分带。

4.2.1 6°分带法

从格林威治零度经线起，每6°分为一个投影带，全球共分为60个投影带，东半球从东经0°—6°为第一带，中央经线为3°，依此类推，投影带号为1—30。其投影代号n和中央经线经度L0的计算公式为：L0=(6n—3)°；西半球投影带从180°回算到0°，编号为31—60，投影代号n和中央经线经度L0的计算公式为L0=360—(6n—3)°。

4.2.2 3°分带法

从东经1°30′起，每3°为一带，将全球划分为120个投影带，东经1°30′—4°30′，…178°30′—西经178°30′，…1°30′—东经1°30′。
东半球有60个投影带，编号1—60，各带中央经线计算公式：L0=3°n，中央经线为3°、6°…180°。西半球有60个投影带，编号1—60，各带中央经线计算公式：L0=360°—3°n，中央经线为西经177°、…3°、0°。