本文详细介绍了惯性矩和惯性积的平行移轴公式，包括使用条件和计算方法，并通过例题解析了组合截面的惯性矩。此外，还探讨了惯性矩与惯性积的转轴公式，讨论了主惯性轴、主惯性矩的概念及其计算，以及如何确定形心主轴和形心主矩。
12.3惯性矩和惯性积的平行移轴公式(
一、组合截面的惯性矩和惯性积
1、惯性矩和惯性积的平行移轴公式
注意，下图例子中，z轴与z'轴不同，需要平移
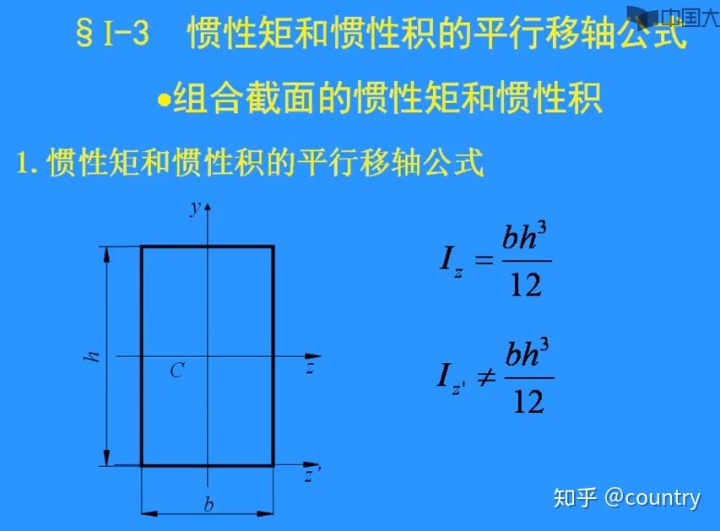
2、惯性矩和惯性积的平行移轴公式使用条件：
1）两轴必须平行；
2）在两根轴中有一根必须是形心轴。
3）a、b是形心C在yoz坐标系中的坐标，可正可负
4）在一组平行轴系中，平面图形对形心轴的惯性积最小
二、例题：求图示T型截面对水平形心轴的惯性矩
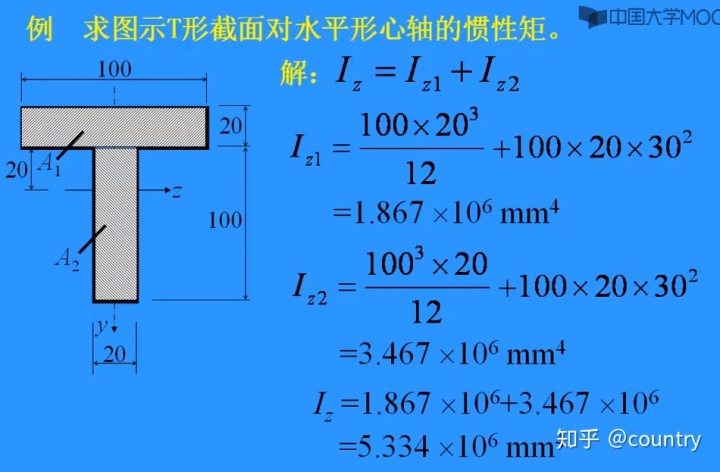
12.3.1组合截面的惯性矩
一、例题：求图示截面对其形心轴的惯性矩
1、解法一：
注：
1）右下角1表示第一个子块，即axa的矩形；2则表示第二个子块，即直径为a的半圆
2）Zc'为过形心的Z轴，位置上图求yc时已求出
2、解法二：
12.4惯性矩与惯性积的转轴公式(
一、截面的主惯性轴和主惯性矩
1、惯性矩和惯性积的转轴公式：
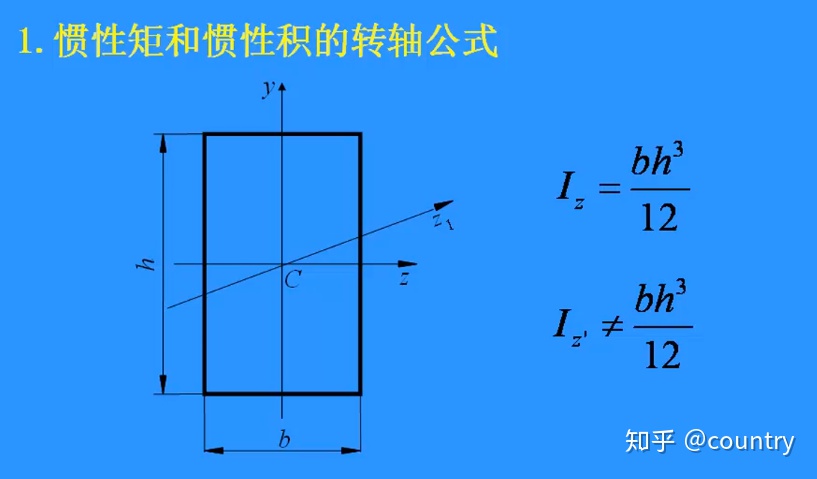
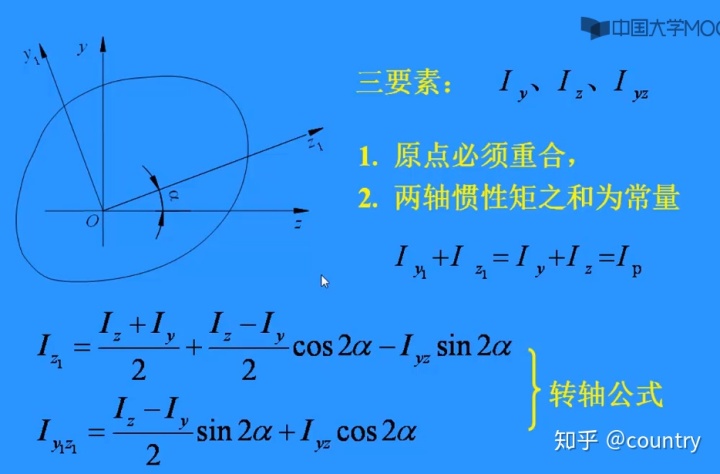
2、三要素：Iy、Iz、Iyz；倾斜角α，逆时针为正
3、使用前提：
1）转动时原点必须重合
2）两轴惯性矩之和为常量
12.4.1利用转轴公式计算惯性矩
一、例题：直径为d的四分之一圆形，C是其形心，求Iz？
1、解法一：先平移，后四矩式
2、解法二：先转动，再平移
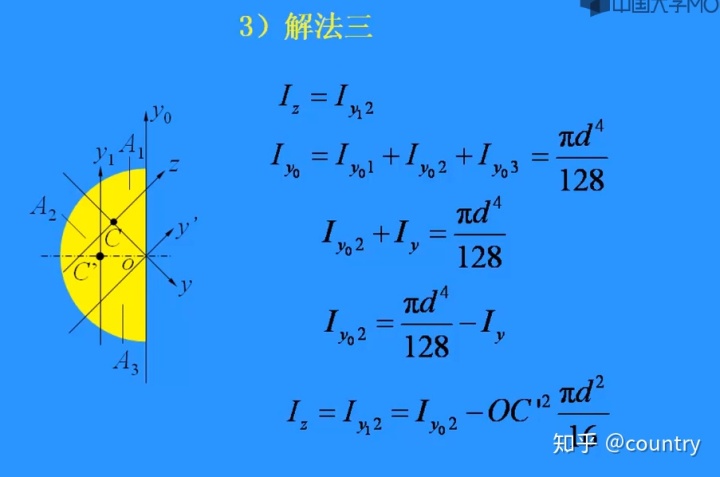
3、解法三：添加另外一个半圆，求夹在中间扇形的惯性矩
12.4.2主轴和主矩
一、截面的主惯性轴和主惯性矩
1、主惯性轴：图形对其惯性积为0的一对坐标轴
2、主惯性矩：截面对于主惯性轴的惯性矩，简称主矩
3、过同一点的轴系中，主轴可能不唯一，但主矩是唯一的
4、过不同点的轴系中，主轴和主矩都是不同的，其大小与所取的坐标原点相关
二、形心主轴和形心主矩
1、形心主惯性轴：主惯性轴的原点与形心重合，简称形心主轴
2、形心主惯性矩：截面对于形心主惯性轴的惯性矩，简称形心主矩
3、两点结论：
1）形心主矩中的极小值一定是一个图形所有惯性矩中的的最小值。较小形心主矩是最小值
2）形心主矩中的极大值不是一个图形所有惯性矩中的的最大值。较大的形心主矩不是最大值
三、形心主轴和形心主矩的确定
1、当一个平面图形（截面）有三根或以上的对称轴时，则过形心的任一根轴均为形心主轴，且惯性矩相等。最常见的图形为正多边形和圆
2、若一个图形（截面）仅有两根互相垂直的对称轴，则这两根轴一定是形心主轴。最常见的为矩形和工字形。
3、若一个图形（截面）仅有一根对称轴时，该对称轴时一根形心主轴，另一根形心主轴与该轴垂直。常见的为T型轴和U型轴
4、无对称轴，只能正常计算
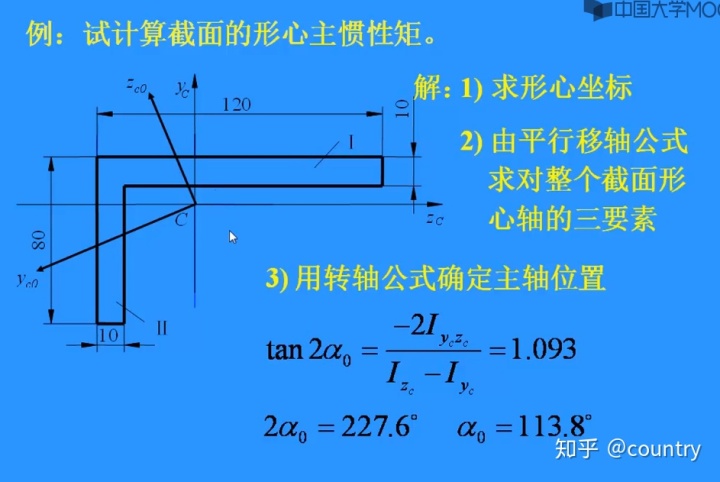
四、例题：试计算截面的形心主惯性矩（无对称轴）
步骤：
1）求形心坐标
2）过形心做初始坐标轴
3）由平行移轴公式求对整个截面形心轴的三要素Iy、Iz、Iyz
4）用转轴公式确定主轴位置
5）利用三要素求出形心主轴和形心主矩
12.4.3组合截面的主轴和主矩
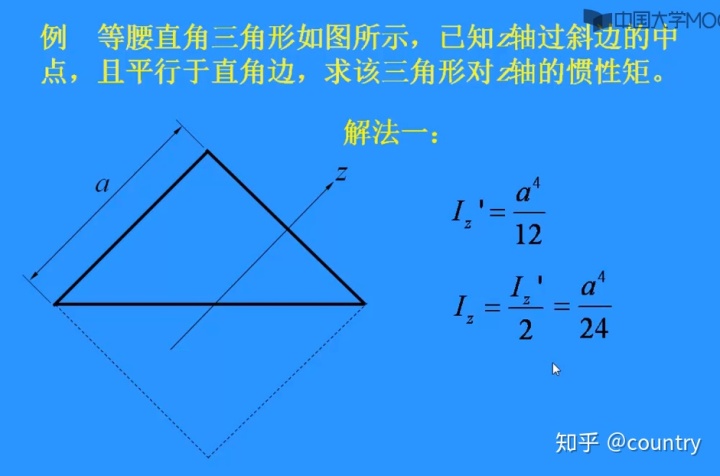
一、例题：求该三角形对z轴的惯性矩
1、解法一：补足另一半三角形，形成一个正方形
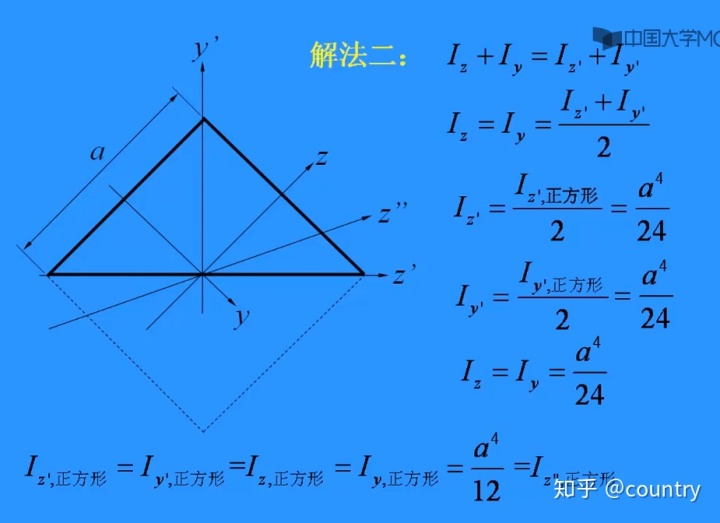
2、解法二：转动z轴，至z'，形成y'z'坐标系
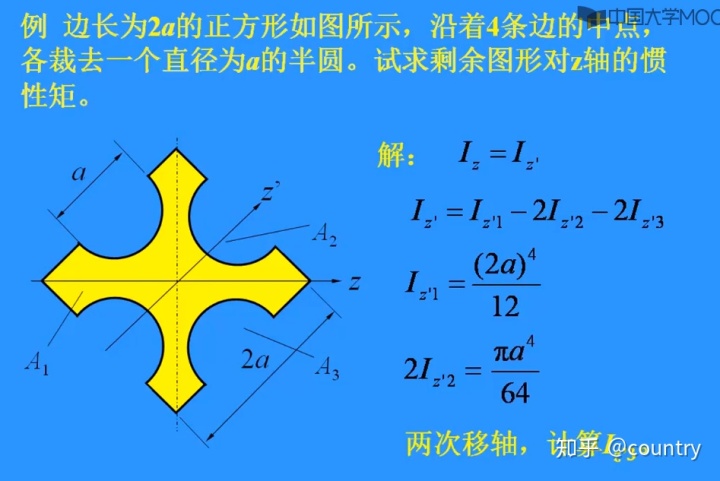
二、例题：试求剩余图形对z轴的惯性矩
注意：因为此图形的对称轴有四根，根据定理（当一个平面图形（截面）有三根或以上的对称轴时，则过形心的任一根轴均为形心主轴，且惯性矩相等。最常见的图形为正多边形和圆）
三、截面的几何性质小结：
1、静矩和形心
1）任意形状的平面图形，对其形心轴的静矩为0；静矩为0的轴，肯定是形心轴。
静矩（Sz）为0
2）形心轴划分出来的两个子块，他们各自对形心轴的静矩大小相等，符号相反
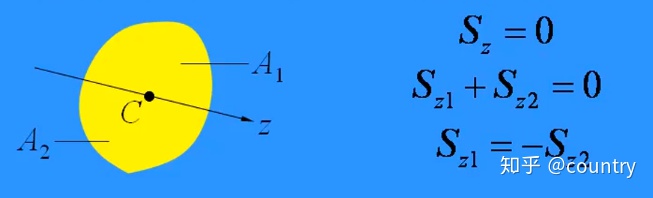
3）对称轴左右的两个部分，各自对形心轴的静矩皆为0
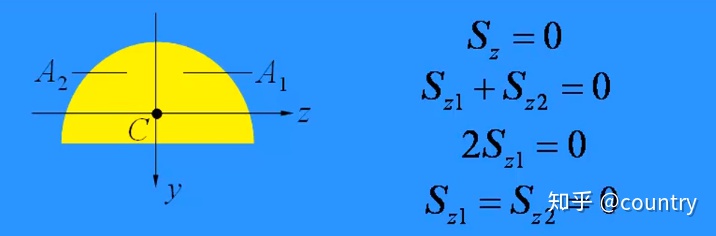
2、惯性矩和惯性积
1）记住矩形、三角形、圆形的惯性矩
2）惯性矩的四矩式
3）平移公式
注意两点：
·1个形心轴+1个非形心轴，平移公式可用
2个非形心轴，平移公式不可用
·若平移公式可用，需确定移轴项符号，是正还是负
3、形心主轴和形心主矩
附录第二部分完
扫一扫
1895
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
