covariance 公式_协方差（covariance）与相关系数（1）

于 2020-11-30 16:45:23 发布 · 8.5k 阅读

文章标签：

#covariance 公式

本文介绍了协方差的概念及其在描述正向、负向和无相关趋势中的作用。通过计算和举例说明，强调协方差对数据尺度的敏感性，并指出相关系数作为其不敏感于尺度的替代指标。文章总结了协方差在分析中的应用，并预告了后续关于计算相关系数的内容。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.三类关系趋势

如下，在测量5个肝细胞gene x 转录本表达情况的基础上，同时也测量这5个肝细胞gene y转录本表达量。对来自同一细胞(sample)的两个数据进行配对，利用其在X轴(green)和Y轴(red)上的数据在二维平面组成一个新的点(蓝色的点)并用直线对其进行拟合。

1)如果斜率(slope)为正，gene x与gene y在细胞中表达成正相关。gene x表达水平随gene Y表达水平的增加而增加。利用拟合的直线，可以根据gene x的表达量预测gene y表达水平，也可以基于gene y的表达量预测gene x的表达水平。
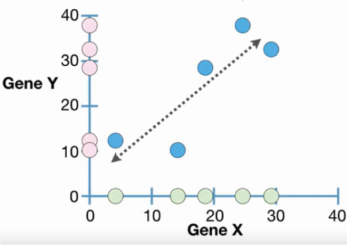
2)如果斜率为负，Gene x与gene y的表达呈现负相关趋势。较低的gene x表达水平对应较高的gene y表达水平，较高的gene x水平对应较低的gene y表达水平。
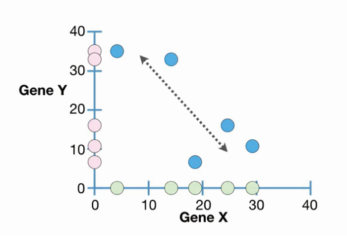
3)如果斜率为0或者斜率不存在，gene x与gene y的表达水平之间无关联。表现为gene y/x的表达水平不随gene x/y的表达量变化而变化。

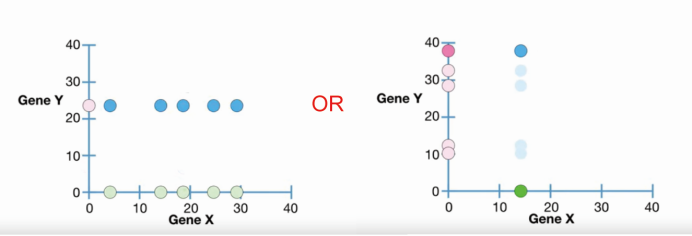
小结：covariance 的主要思想之一，其可以将数据分为三类关系：正向趋势的关系；负向趋势的关系；无任何趋势的关系。

2. 协方差描述三类关系趋势

「如何计算covariance：」

协方差的计算公式：

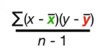
「当协方差为正时，gene x与gene y两变量间表现为正相关性。」 依次将数据代入公式，可以发现：两个黄色象限(一、三象限)的样本都对整体协方差做成正的贡献。协方差为116，它意味着gene x与gene y之间的拟合相关直线斜率是正值。因此，可以得出这样的结论：当协方差为正时，gene x与gene y之间呈正的变化趋势。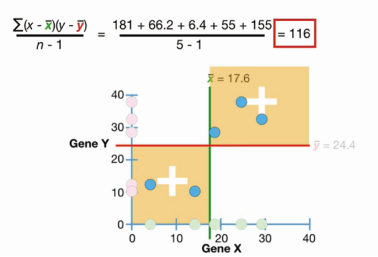

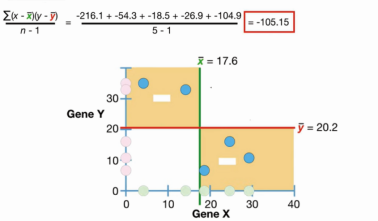
「当协方差为负，gene x与gene y两变量间表现为负相关性。」 假设gene y的值与前不同，gene y的样本均值为20.2。Gene x的值保持不变，gene x的均值为17.6。我们使用协方差的计算公式计算gene x与gene y的协方差，在黄色象限的数据对整体协方差做出负的贡献，最后协方差等于-105.15。因此可以得出结论：当协方差为负时，gene x与gene y两变量间的相关性直线的斜率为负。

「将协方差为0时，gene x与gene y两变量间表现为无相关性。」 同样的计算方法，我们可以推算出，当gene x与gene y表达水平无关系时，协方差等于0。因此可以得出结论：当协方差为0时，gene x与gene y两变量间无相关关系。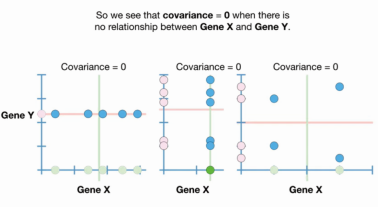

注意！！！协方差本身并不容易被阐释，它不能告诉我们相关性直线的斜率(陡峭或平坦)，也不能告诉我们样本是否靠近相关性直线，它仅仅告诉我们两变量之间的相关性直线的斜率是正还是负。

3.协方差对数据的scale敏感

协方差本身的意义难以诠释，故我们不会以计算协方差为目标。但是计算协方差是其他计算的基础，例如相关系数(correlation)。

「协方差对数据的scale敏感，使其不能揭示数据间的相关性程度。」

例如，计算gene x与gene x的协方差，带入公式可得102；将gene x的表达水平扩大2倍后，求得gene x与其自身的协方差为408，是原来数据的4倍(如下)。故协方差对数据的scale非常敏感，此造成了协方差本身的难以阐释。
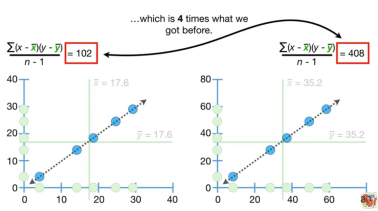
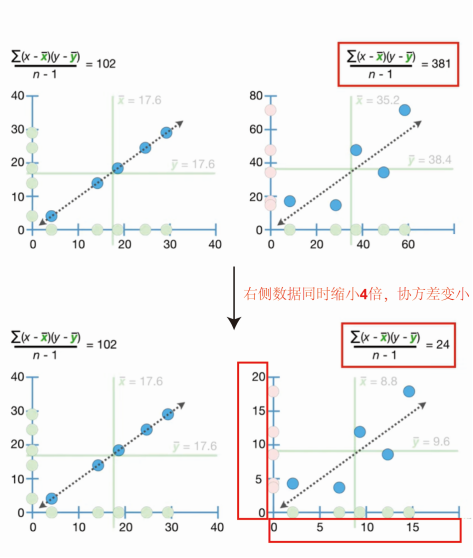
又例如：左边的数据较右边的数据更接近相关性直线，左边数据对应的协方差为102；右边数据对应的协方差为381，远大于左侧数据的协方差。将右侧数据同时缩小4倍后，数据距离相关性直线的距离未发生改变，但对应的协方差变为24，小于原来的协方差，也小于左侧数据的协方差。