幂级数和函数经典例题_考研数学三级数~求幂级数的收敛域、和函数、幂级数展开式问题总结...

一、求幂级数的收敛半径

求收敛半径是求幂级数的和函数和展开式的基础，在数三09年中考察了一道求幂级数收敛半径的填空题，

求收敛半径通常包括以下几种类型:

1)该幂级数缺少偶数项或奇数项;

eg:

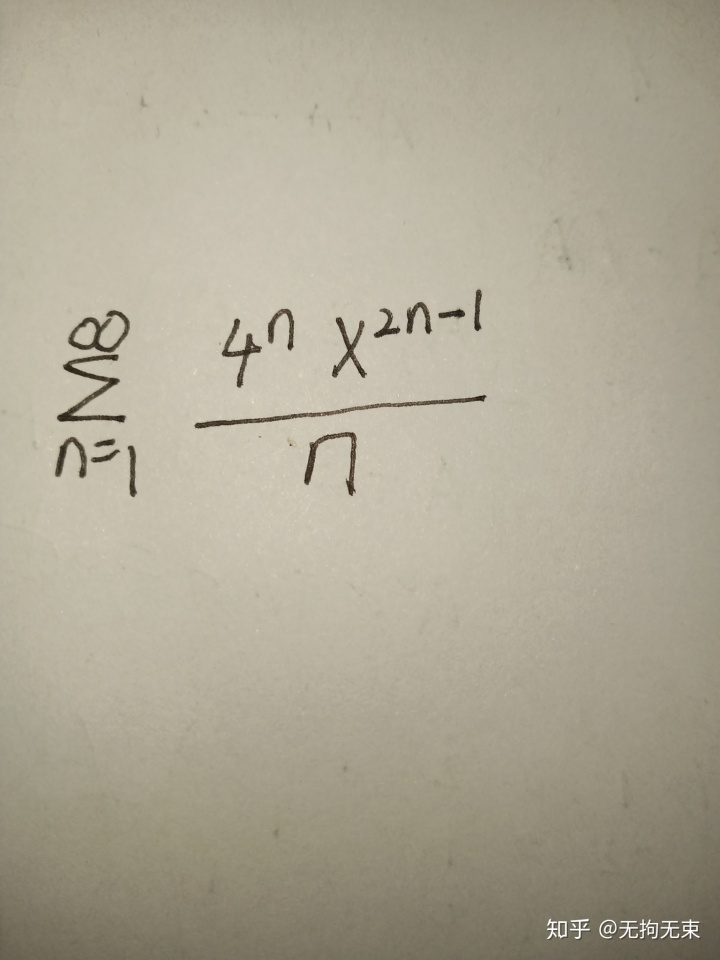
显然上面的幂级数缺少偶次项，这时，我们可以将x看成一个常数，把原幂级数当作一个数项级数来处理，即:

在数三的近20年考试中，这种类型的题目出现了2次，分别是2006年;2016年

2)幂级数中的x项为(x+c)的形式;

eg:

3)在第2种类型的基础上延伸，给出x在某一点处收敛或发散，然后求常数;

eg:

二、求幂级数的和函数需要注意的问题

和函数考的频率较高，在05年、06年、14年、16年，都是直接求幂级数的和函数，17年是将和函数与微分方程结合起来考的，所以大家一定要掌握好这部分的内容。

在求和函数时，一定要先求收敛域，先求收敛域，先求收敛域，这一点很容易忘，大家一定要牢记。

1)可能需要先对幂级数进行拆解;

eg:

2)可能是先积分(有可能需要积2次分)后求导;

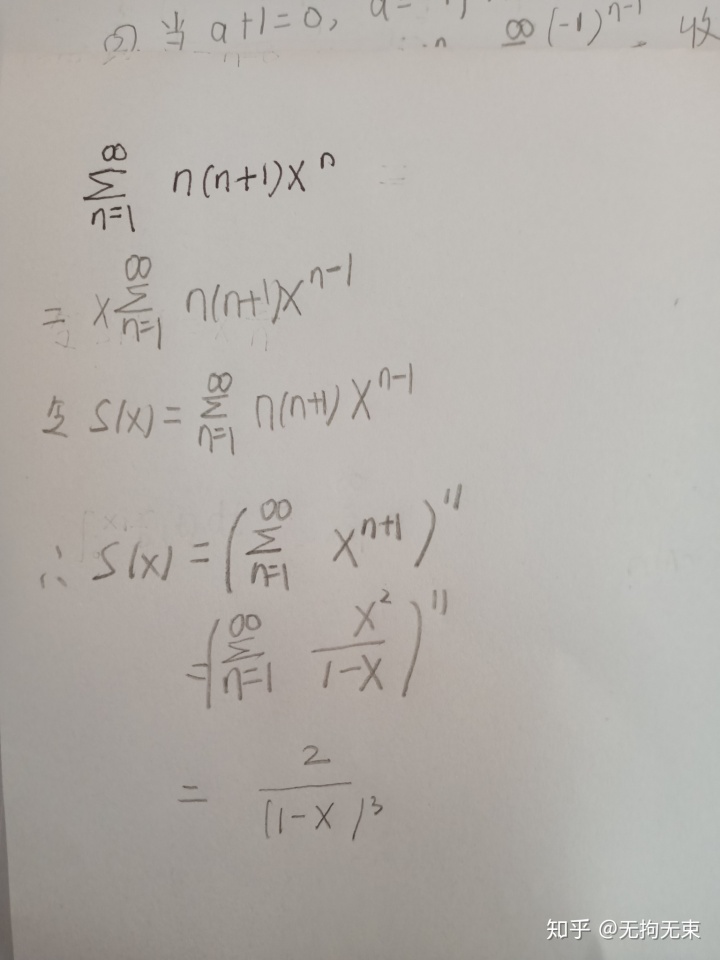
3)先求导再积分，涉及求S(0)的问题;

关于S(0)的问题，只有在出现分母的情况下，才需要求S(0),If幂级数没有分母，那么则不要考虑S(0);

在下面这个例题中，虽然也是先求导在积分，但无需考虑S(0);

eg:

其次，我们要搞清楚S(0)表示的含义，s(0)表示数列An的第一项，如果n是从0开始的，幂级数为X^n时，此时第一项就A0，s(0)=A0;

如果幂级数为X^(n+1),此时第一项就A0*X，那么S(0)就是0;即如果第一项有x,那S(0)就一定是0。

下面举几个例题:

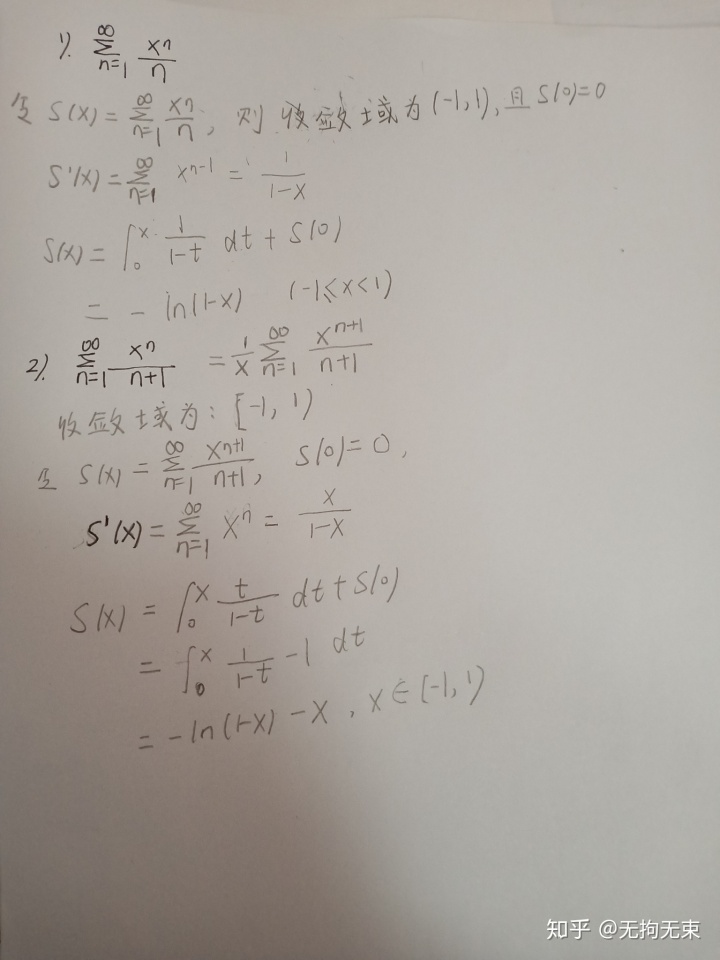
4)注意最后求的和函数的收敛域，可能会发生改变;

在逐项求导过程中，收敛域可能会缩小;

在逐项积分的过程中，收敛域可能会扩大

三、求幂级数的展开式

幂级数的展开式在考试中出现了2次，一次是07年，一次是18年，

幂级数的展开式主要包括两种类型:

1)求幂级数在指定点的展开式，比如求f(x)在x=1,x=3处的展开式;

这种类型的展开式，相对来说比较简单，通常就是在函数那做做文章，需要先对函数拆解，比如1/x^2+3x+2, ln[2x^2+x+3],只需要对函数因式分解即可;

2)求幂级数在x处的展开式;

这种类型考的比较多，出题也比较灵活，大家首先要牢记常见的7个麦克劳林展开式，

这是做对这种题的基础，然后常见的几种套路有:

A.函数当中的x比较复杂，需要对x先化简;

eg1: f(x)=ln[1+x+x^2];

eg2: f(x)=arctan(1+x)/(1－x)

第一个考察的是立方差公式，x^3－1=(x-1)(x^2+x+1);

第二个是首先需要对f(x)求导，然后在积分即可。

B.f(x)比较复杂，是多项式的组合，包括2个式子相加、2个式子相减等;

这种多项式里面通常是包含一个常见的麦克劳林级数，然后与另一个式子相乘/相除，所以我们首先算出这个麦克劳林级数的展开式，然后在相加减即可，下面来举例说明:

C.f(x)中除了涉及幂级数的展开式外，还设计求导或积分;

最后，还有几个几何级数求和公式以及由它导出的几个常见的公式，大家最好也要记住:

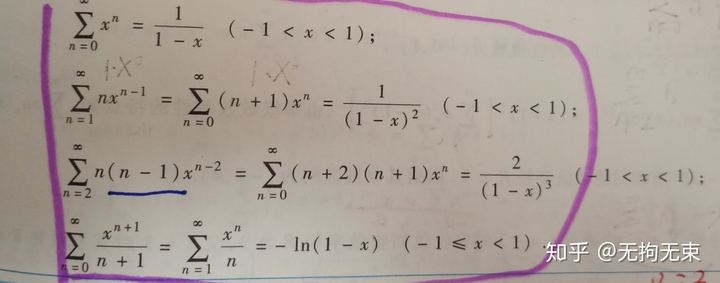
好了，今天的分享就到这里了，关于级数收敛的判定，下次再说，如果你觉得对你有帮助的话，就给点个赞吧！