直角坐标积分化为极坐标积分_重积分这一章应该掌握的内容（已含考研内容）...

首先把这这一章主要应该背记的公式展示一下，使得看下面具体内容时可以知道各个公式当中包含了那些内容。

下面的主要内容来自我编写的一本书，其封面如下：

由于重积分是其他多元积分的基础，所以内容比较多，因此我们会把它分成一个一个的文章，使得读者各取所需，并能够比较快地找到自己想看的内容。

先给出二重积分的定义：

三重积分的定义：

然后是基本内容和基本例题的安排：

接着是

https://zhuanlan.zhihu.com/p/109410287​zhuanlan.zhihu.com

接下来就是(1)将二重积分化为极坐标下的二次积分，(2)重积分的奇偶对称性，(3)二重积分相关的积分的互化，(4)如何计算分块函数的二重积分：

https://zhuanlan.zhihu.com/p/112148826​zhuanlan.zhihu.com

下面是三重积分的计算。其中包括:

(1)用先一后二法计算三重积分;

(2)用先二后一法计算三重积分;

(3)用柱坐标系计算三重积分;

(4)用球坐标系计算三重积分;

(5)重积分计算公式的微元法解释。

https://zhuanlan.zhihu.com/p/112183736​zhuanlan.zhihu.com

下面讲重积分的轮换对称性及相关例题：

从上一张照片的最后两行开始，讲的是直角坐标系中的累次积分化为球坐标系中的累次积分的题目：

下面是一个初等函数的累次积分，需要交换积分次序才能做出来的题目，接着的也是交换累次积分次序的题目：

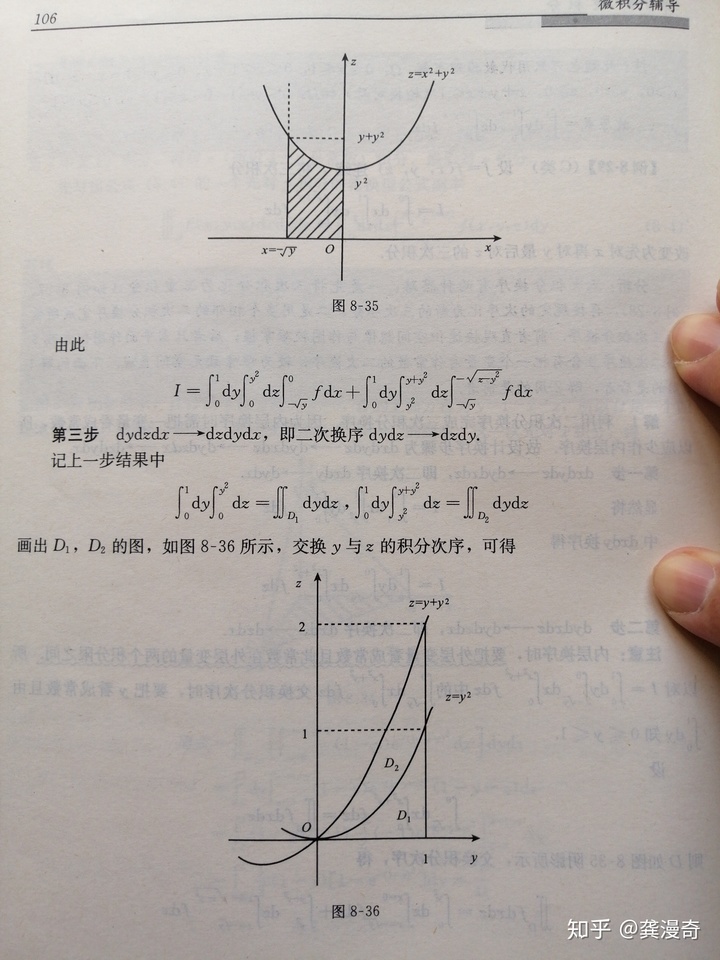
从上一张照片的例8-31开始是含参重积分（其中参数在积分域当中）的相关问题：

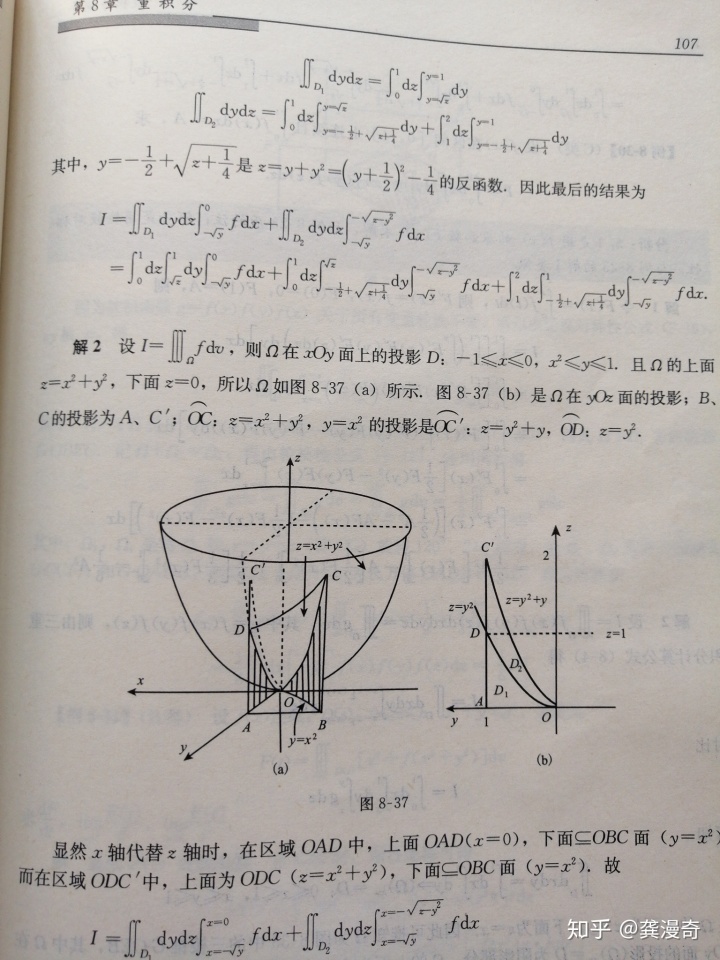
上一张照片中的例8-35是一个围积分区域的方程中有三个含z方程的三重积分，如何求解的问题：

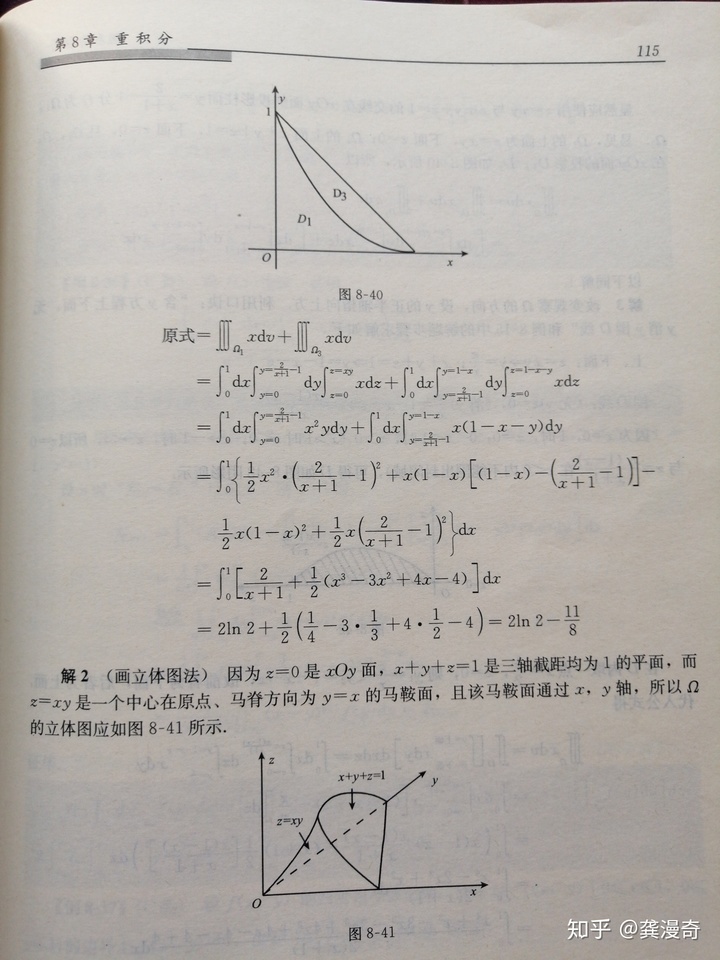
上一张照片中的例8-36是一个n次累次积分化定积分的问题。而其中的例3-37是一个函数在矩形区域的边界上函数值为零，中间的高阶导数值有界的情况下，估计该二重积分的界的题目。

下面的链接是重积分的微元法以及重积分应用的例题。

https://zhuanlan.zhihu.com/p/112433437​zhuanlan.zhihu.com

下面是有有关重积分换元的内容：

https://zhuanlan.zhihu.com/p/112442535​zhuanlan.zhihu.com

下面是一些习题及其答案。

下面这这部分内容是为考研究生的学生准备的：这个内容已经写在我写的一篇文章《曲线曲面积分这一章应掌握的内容》的最后一部分。