模型集成与融合

目录

1 集成方法(Ensemble Method)

2 集成学习的主要方法

2.1 Bagging（Boostrap Aggregating，装袋）

2.1.1 Bagging概述

2.1.2 随机森林

2.2 Boosting

2.2.1 Boosting算法的发展历史

2.2.2 Boosting概述

2.2.3 Boosting的两个核心问题

2.2.4 AdaBoost

2.2.5 GBDT​​​​​​​

2.3 Stacking

2.4 Blending

2.5 方法对比

2.5.1 Bagging，Boosting的主要区别

2.5.2 Blending与Stacking对比

3 常见问题

3.1 常用的基分类器是什么？

3.2 可否将随机森林中的基分类器， 由决策树替换为线性分类器或K-近邻？ 请解释为什么？

3.3 如何从减小方差和偏差的角度解释Boosting和Bagging的原理？

3.3.1  Bagging降低了方差

3.3.2 Boosting 降低了偏差

---

1 集成方法(Ensemble Method)

        集成学习是一种机器学习范式。在集成学习中，我们会训练多个模型（通常称为「弱学习器」）解决相同的问题，并将它们结合起来以获得更好的结果。最重要的假设是：当弱模型被正确组合时，我们可以得到更精确和/或更鲁棒的模型。

        集成学习理论中，我们将弱学习器（或基础模型）称为「模型」，这些模型可用作设计更复杂模型的构件。在大多数情况下，这些基本模型本身的性能并不是非常好，这要么是因为它们具有较高的偏置（例如，低自由度模型），要么是因为他们的方差太大导致鲁棒性不强（例如，高自由度模型）。

        集成方法的思想是通过将这些弱学习器的偏置和/或方差结合起来，从而创建一个「强学习器」（或「集成模型」），从而获得更好的性能。

        组合弱学习器：

        为了建立一个集成学习方法，我们首先要选择待聚合的基础模型。在大多数情况下（包括在众所周知的 bagging 和 boosting 方法中），我们会使用单一的基础学习算法，这样一来我们就有了以不同方式训练的同质弱学习器。

        这样得到的集成模型被称为「同质的」。然而，也有一些方法使用不同种类的基础学习算法：将一些异质的弱学习器组合成「异质集成模型」。

        很重要的一点是：我们对弱学习器的选择应该和我们聚合这些模型的方式相一致。如果我们选择具有低偏置（偏差）高方差的基础模型，我们应该使用一种倾向于减小方差的聚合方法；而如果我们选择具有低方差高偏置（偏差）的基础模型，我们应该使用一种倾向于减小偏置（偏差）的聚合方法。

        这就引出了如何组合这些模型的问题。我们可以用四种主要的旨在组合弱学习器的「元算法」：

       集成方法主要包括Bagging（套袋法）和Boosting（提升法）两种方法。

• Bagging（套袋法）：该方法通常考虑的是同质弱学习器，相互独立地并行学习这些弱学习器，并按照某种确定性的平均过程将它们组合起来。在Bagging方法中，主要通过对训练数据集进行随机采样，以重新组合成不同的数据集，利用弱学习算法对不同的新数据集进行学习，得到一系列的预测结果，对这些预测结果做平均或者投票做出最终的预测。随机森林算法(RandomForest) 是基于Bagging思想的机器学习算法。
•  Boosting（提升法）：该方法通常考虑的也是同质弱学习器。它以一种高度自适应的方法顺序地学习这些弱学习器（每个基础模型都依赖于前面的模型），并按照某种确定性的策略将它们组合起来。在Boosting思想中是通过对样本进行不同的赋值，对错误学习的样本的权重设置的较大，这样，在后续的学习中集中处理难学的样本，最终得到一系列的预测结果，每个预测结果有一个权重，较大的权重表示该预测效果较好。AdaBoost算法和GBDT(Gradient Boost Decision Tree，梯度提升决策树)算法是基于Boosting思想的机器学习算法。
• stacking：该方法通常考虑的是异质弱学习器，并行地学习它们，并通过训练一个「元模型」将它们组合起来，根据不同弱模型的预测结果输出一个最终的预测结果。
• Blending：Blending与Stacking大致相同，只是Blending的主要区别在于训练集不是通过K-Fold的CV策略来获得预测值从而生成第二阶段模型的特征，而是建立一个Holdout集，例如10%的训练数据，第二阶段的stacker模型就基于第一阶段模型对这10%训练数据的预测值进行拟合。说白了，就是把Stacking流程中的K-Fold CV 改成 HoldOut CV。

注：

        在概率近似正确(probably approximately correct， PAC)学习的框架中，一个概念(一个类)，如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的。一个概念，如果存在一个多项式的学习算法能够学习它，学习正确率仅比随机猜测略好，那么就称这个概念是弱可学习的。Schapire指出在PAC学习框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。那么对于一个学习问题，若是找到“弱学习算法”，那么可以将弱学习方法变成“强学习算法”。

2 集成学习的主要方法

2.1 Bagging（Boostrap Aggregating，装袋）

2.1.1 Bagging概述

        多个模型投票或者取平均值（Bagging）。

        对于数据集训练多个模型，对于分类问题，可以采用投票的方法，选择票数最多的类别作为最终的类别，而对于回归问题，可以采用取均值的方法，取得的均值作为最终的结果。在这样的思路里最著名的是Bagging方法。Bagging即Boostrap Aggregating，其中，Boostrap是一种有放回的抽样方法，其抽样策略是简单的随机抽样。

        在Bagging方法中，让学习算法训练多次，每次的训练集由初始的训练集中随机取出的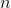个训练样本组成，初始的训练样本在某次的训练集中可能出现多次或者根本不出现。最终训练出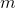个预测函数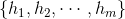，最终的预测函数为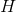，对于分类和回归问题可采用如下的两种方法：

1. 分类问题：采用投票的方法，得票最多的类别为最终的类别
2. 回归问题：采用简单的平均方法，取得的均值作为最终的结果。

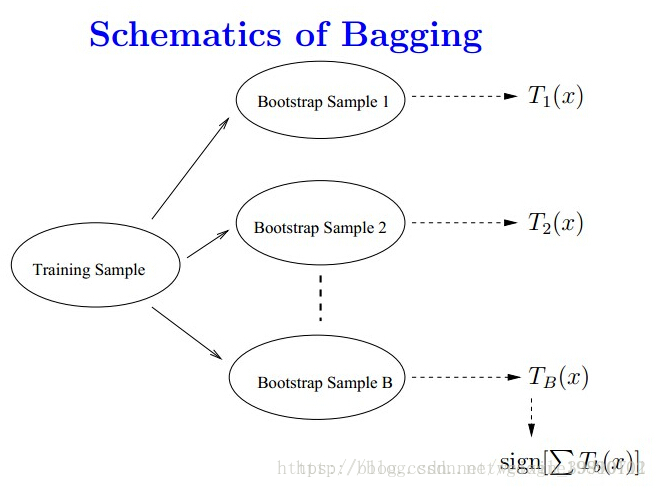
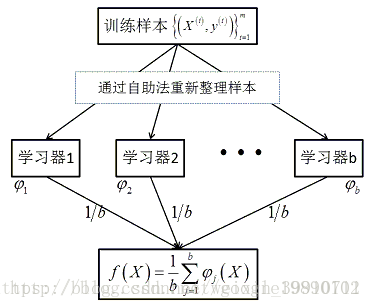
bagging的算法过程如下：

1. 从原始样本集中使用Bootstraping方法随机抽取n个训练样本（有放回）（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中），共进行k轮抽取，得到k个训练集（k个训练集之间相互独立，元素可以有重复）。
2. 每次使用一个训练集得到一个模型。对于k个训练集，我们训练k个模型（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）
3. 对于分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

            

        bagging方法总结：

　　①  Bagging通过降低基分类器的方差，改善了泛化误差
　　②  其性能依赖于基分类器的稳定性；如果基分类器不稳定，bagging有助于降低训练数据的随机波动导致的误差；如果稳定，则集成分类器的误差主要由基分类器的偏倚引起
　　③  由于每个样本被选中的概率相同，因此bagging并不侧重于训练数据集中的任何特定实例

        随机森林算法就是基于Bagging思想的学习算法。

2.1.2 随机森林

        在随机森林中，集成中的每棵树都是由从训练集中抽取的样本（即 bootstrap 样本）构建的。另外，与使用所有特征不同，这里随机选择特征子集，从而进一步达到对树的随机化目的。

        因此，随机森林产生的偏差略有增加，但是由于对相关性较小的树计算平均值，估计方差减小了，导致模型的整体效果更好。            

       随机森林分解开来就是“随机”和“森林”。

• 随机：随机森林的随机性：

        1. 数据集的随机选取：从原始的数据集中采取有放回的抽样（bagging），构造子数据集，子数据集的数据量是和原始数据集相同的。不同子数据集的元素可以重复，同一个子数据集中的元素也可以重复。

        2. 待选特征的随机选取：与数据集的随机选取类似，随机森林中的子树的每一个分裂过程并未用到所有的待选特征，而是从所有的待选特征中随机选取一定的特征，之后再在随机选取的特征中选取最优的特征。

• 森林：森林是由很多棵树组成的，因此随机森林的结果是依赖于多棵决策树的结果，这是一种集成学习的思想。

        随机森林的构建过程：

1. 从原始训练集中使用Bootstraping方法随机有放回采样取出m个样本，共进行n_tree次采样。生成n_tree个训练集；
2. 对n_tree个训练集，我们分别训练n_tree个决策树模型；
3. 对于单个决策树模型，假设训练样本特征的个数为n，那么每次分裂时根据信息增益/信息增益比/基尼指数选择最好的特征进行分裂；
4. 每棵树都已知这样分裂下去，直到该节点的所有训练样例都属于同一类。在决策树的分裂过程中不需要剪枝；
5. 将生成的多颗决策树组成随机森林。对于分类问题，按照多棵树分类器投票决定最终分类结果；对于回归问题，由多颗树预测值的均值决定最终预测结果。

        注意：OOB（out-of-bag ）：每棵决策树的生成都需要自助采样，这时就有1/3的数据未被选中，这部分数据就称为袋外数据。

2.2 Boosting

2.2.1 Boosting算法的发展历史

        boost 算法系列的起源来自于PAC Learnability(PAC 可学习性)。

        Boosting算法是一种把若干个分类器整合为一个分类器的方法，在boosting算法产生之前，还出现过两种比较重要的将多个分类器整合为一个分类器的方法，即boostrapping方法和bagging方法。我们先简要介绍一下bootstrapping方法和bagging方法。

　　1）bootstrapping方法的主要过程

　　主要步骤：

1. 重复地从一个样本集合D中采样n个样本
2. 针对每次采样的子样本集，进行统计学习，获得假设Hi
3. 将若干个假设进行组合，形成最终的假设Hfinal
4. 将最终的假设用于具体的分类任务

　　2）bagging方法的主要过程

       bagging可以有多种抽取方法（见本文2.1）

　　主要思路：

1. 训练分类器：从整体样本集合中，抽样n* < N个样本 针对抽样的集合训练分类器Ci
2. 分类器进行投票，最终的结果是分类器投票的优胜结果

　　但是，上述这两种方法，都只是将分类器进行简单的组合，实际上，并没有发挥出分类器组合的威力来。直到1989年，Yoav Freund与 Robert Schapire提出了一种可行的将弱分类器组合为强分类器的方法。并由此而获得了2003年的哥德尔奖（Godel price）。

       3）早期的boosting算法

　　Schapire还提出了一种早期的boosting算法，其主要过程如下：

1. 从样本整体集合D中，不放回的随机抽样n1 < n个样本，得到集合 D1，训练弱分类器C1
2. 从样本整体集合D中，抽取 n2 < n个样本，其中合并进一半被C1 分类错误的样本。得到样本集合D2，训练弱分类器C2
3. 抽取D样本集合中，C1 和 C2 分类不一致样本，组成D3，训练弱分类器C3
4. 用三个分类器做投票，得到最后分类结果

       4）现在的adaboost算法

　　到了1995年，Freund and schapire提出了现在的adaboost算法，其主要框架可以描述为：

1. 循环迭代多次：更新样本分布；寻找当前分布下的最优弱分类器；计算弱分类器误差率
2. 聚合多次训练的弱分类器

2.2.2 Boosting概述

        对多个模型的预测结果做加权平均（Boosting）。

        在上述的Bagging方法中，其特点在于随机化抽样，通过反复的抽样训练新的模型，最终在这些模型的基础上取平均。而在对多个模型的预测结果做加权平均则是将多个弱学习模型提升为强学习模型，这就是Boosting的核心思想。

        在Boosting算法中，初始化时对每个训练样本赋予相等的权重，如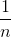，然后用该学习算法对训练集训练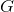轮，每次训练后，对训练失败的训练样本赋予更大的权重，也就是让学习算法在后续的学习中几种对比较难学的训练样本进行学习，从而得到一个预测函数序列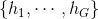，其中每个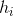都有一个权重，预测效果好的预测函数的权重较大。最终的预测函数为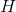对于分类和回归问题可采用如下的两种方法：

1. 分类问题：有权重的投票方式
2. 回归问题：加权平均

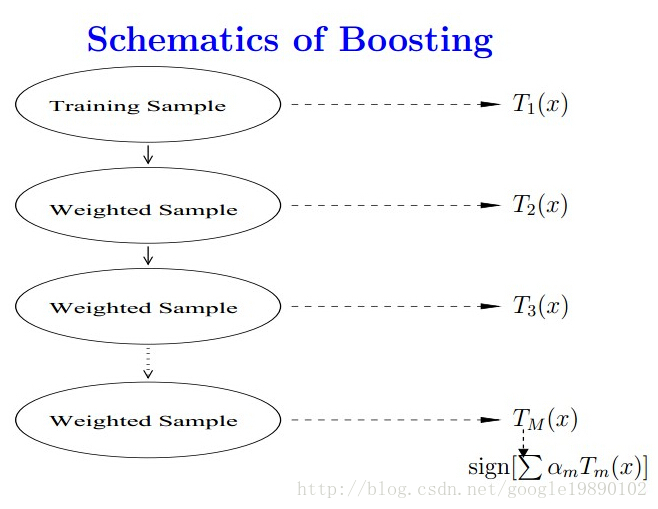
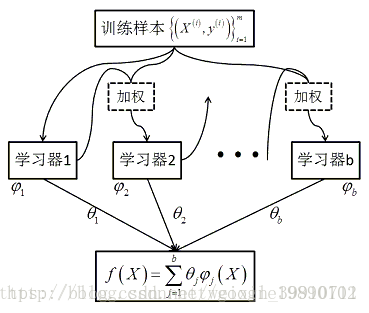
boosting的算法过程如下：

1. 对于训练集中的每个样本建立权值wi，表示对每个样本的关注度。当某个样本被误分类的概率很高时，需要加大对该样本的权值。
2. 进行迭代的过程中，每一步迭代都是一个弱分类器。我们需要用某种策略将其组合，作为最终模型。（例如AdaBoost给每个弱分类器一个权值，将其线性组合最为最终分类器。误差越小的弱分类器，权值越大）

        AdaBoost和GBDT(Gradient Boosting Decision Tree)是基于Boosting思想的两个最著名的算法。

2.2.3 Boosting的两个核心问题

关于Boosting的两个核心问题：

　　1）在每一轮如何改变训练数据的权值或概率分布？

　　通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。

　　2）通过什么方式来组合弱分类器？

        通过加法模型将弱分类器进行线性组合，

2.2.4 AdaBoost

　　AdaBoost（Adaptive boosting）算法：刚开始训练时对每一个训练例赋相等的权重，然后用该算法对训练集训练t轮，每次训练后，对训练失败的训练例赋以较大的权重，也就是让学习算法在每次学习以后更注意学错的样本，从而得到多个预测函数。通过拟合残差的方式逐步减小残差，将每一步生成的模型叠加得到最终模型。

        提升方法（一）：AdaBoost算法：提升方法（一）：AdaBoost算法_意念回复的博客-优快云博客

        Adaboost的基分类器的训练和合并的基本步骤如下。

（1）来源自百面机器学习

 

 （2）

2.2.5 GBDT​​​​​​​

机器学习算法（十五）：GBDT、xgBoost、lightGBM、RF的区别与联系_意念回复的博客-优快云博客_gbdt regression

　　GBDT（Gradient Boost Decision Tree)，每一次的计算是为了减少上一次的残差，GBDT在残差减少（负梯度）的方向上建立一个新的模型。

　　梯度提升决策树， 其核心思想是， 每一棵树学的是之前所有树结论和的残差， 这个残差就是一个加预测值后能得真实值的累加量。我们以一个视频网站的用户画像为例， 为了将广告定向投放给指定年龄的用户， 视频网站需要对每个用户的年龄做出预测。 在这个问题中， 每个样本是一个已知性别/年龄的用户， 而特征则包括这个人访问的时长、 时段、 观看的视频的类型等。
　　例如用户A的真实年龄是25岁， 但第一棵决策树的预测年龄是22岁， 差了3岁， 即残差为3。 那么在第二棵树里我们把A的年龄设为3岁去学习， 如果第二棵树能把A分到3岁的叶子节点， 那两棵树的结果相加就可以得到A的真实年龄； 如果第二棵树的结论是5岁， 则A仍然存在−2岁的残差， 第三棵树里A的年龄就变成−2岁，继续学。 这里使用残差继续学习， 就是GBDT中Gradient Boosted所表达的意思。

          

2.3 Stacking

        合并基分类器的方法有voting和stacking两种。 

　　Stacking方法是指训练一个模型用于组合其他各个模型。首先我们先训练多个不同的模型，然后把之前训练的各个模型的输出为输入来训练一个模型，以得到一个最终的输出。理论上，Stacking可以表示上面提到的两种Ensemble方法，只要我们采用合适的模型组合策略即可。但在实际中，我们通常使用logistic回归作为组合策略。

        使用另外一个机器学习算法来将个体机器学习器的结果结合在一起。在stacking方法中，我们把

• 个体学习器叫做初级学习器，
• 用于结合的学习器叫做次级学习器或元学习器（meta-learner），
• 次级学习器用于训练的数据叫做次级训练集。
• 次级训练集是在训练集上用初级学习器得到的。​​​​​​​

        我们将假设训练数据：train.csv有1000行；测试数据：test.csv有200行。然后按照下图所示训练：

        stacking的步骤：

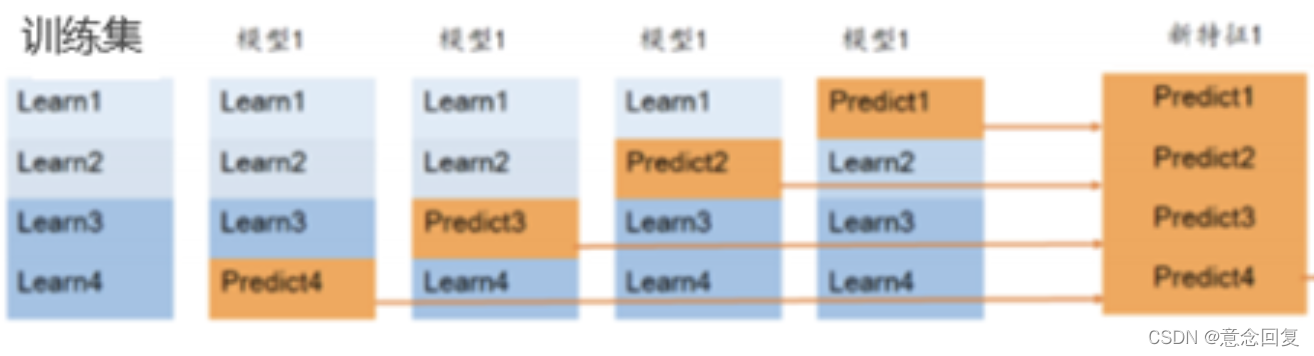
        如图所示，我们现在用4折交叉验证来训练数据，

模型 model1 要做满4次训练：

1. 第一次，model1，拿train.csv的750行做训练集，250行做验证集，然后预测出250行的数据a1。
2. 第二次，model1，拿train.csv的750行做训练集，250行做验证集，然后预测出250行的数据a2。
3. 第三次，model1，拿train.csv的750行做训练集，250行做验证集，然后预测出250行的数据a3。
4. 第四次，model1，拿train.csv的750行做训练集，250行做验证集，然后预测出250行的数据a4。

        然后将a1到a4拼接起来，得到一列，共1000行的数据。

        对于模型2，过程与模型1一样，得到一列1000行数据

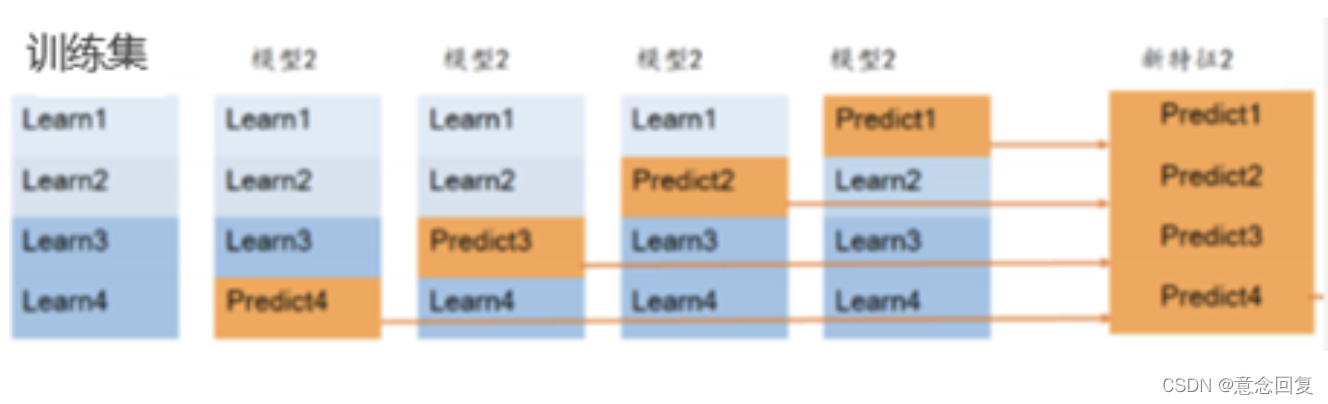
        如果有4个基模型，那么根据train.csv会得到4列数据 ：

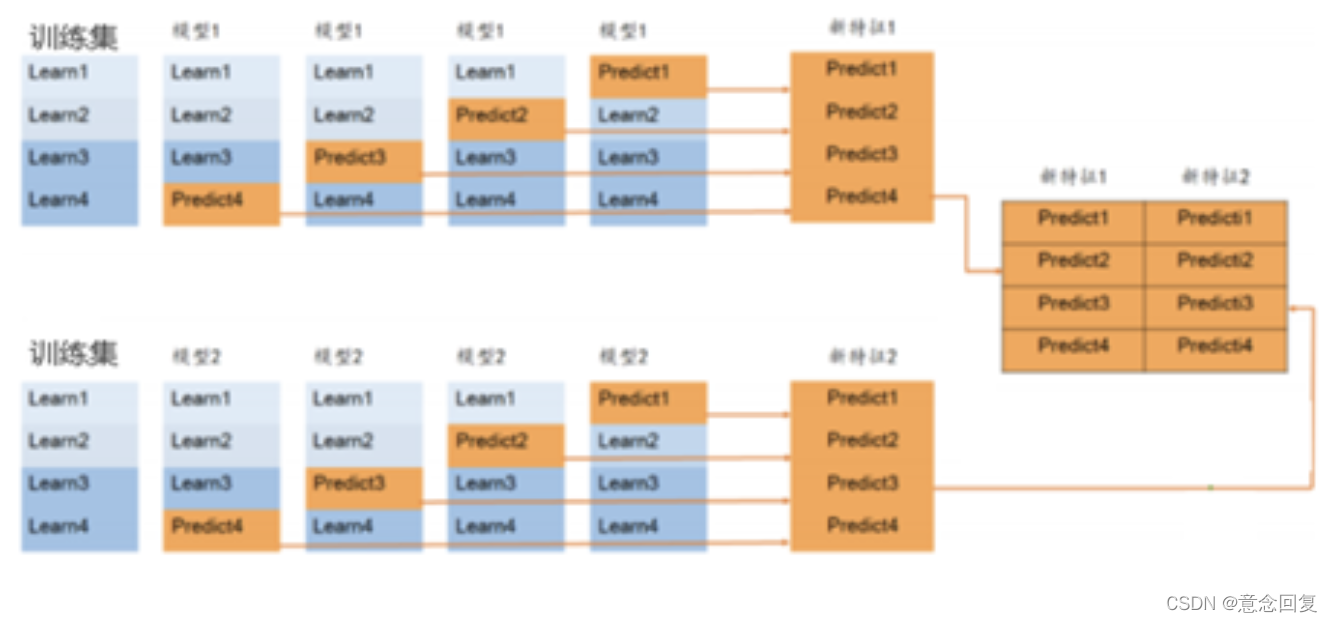
        将预测的结果（新特征）作为次级训练集，放到次级学习器中进行训练。 

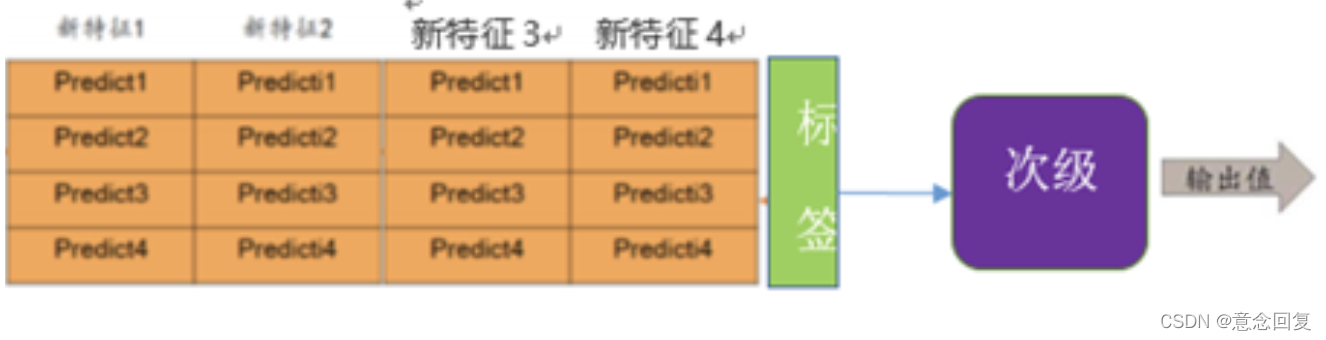
        针对测试集test.csv有两种方法，一种是全部训练完成后，一次性预测输出200行数据；另一种是每个模型每次做完训练就拿test.csv中的数据做预测，一种得到4次200行的数据（每个模型进行4折交叉验证），然后做平均，得到一列200行的数据。
        根据test.csv会得到4列200行的数据，最后，将训练好的模型预测4列200行的数据，得到的最终结果就是最后需要的数据。这仅仅只是2层stacking，多的可以有很多层。然后再放到一个模型中做训练。

        Stacking完整的流程如下： 

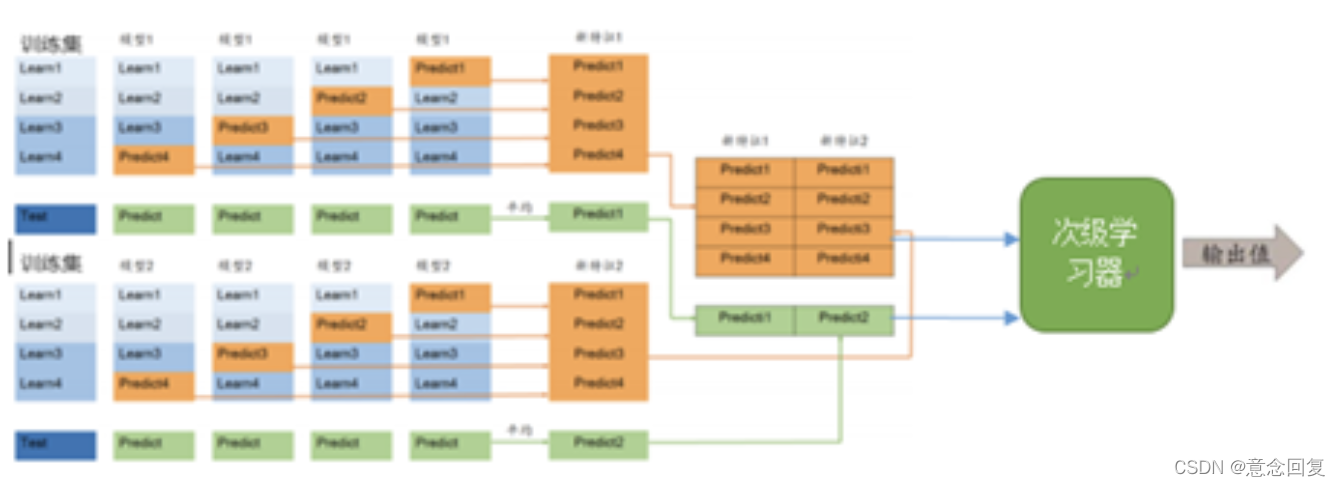
        stacking算法原理：

1. 对于Model1，将训练集D分为k份，对于每一份，用剩余数据集训练模型，然后预测出这一份的结果；
2. 重复上面步骤，直到每一份都预测出来。得到次级模型的训练集；
3. 得到k份测试集，平均后得到次级模型的测试集；
4. 对于Model2、Model3…..重复以上情况，得到M维数据；
5. 选定次级模型，进行训练预测。       

  优缺点：

        优点：

1. 采用交叉验证方法构造，稳健性强；
2. 可以结合多个模型判断结果，进行次级训练，效果好；

       缺点：        

1. 构造复杂，难以得到相应规则，商用上难以解释。

2.4 Blending

        Blending与Stacking大致相同，只是Blending的主要区别在于训练集不是通过K-Fold的CV策略来获得预测值从而生成第二阶段模型的特征，而是建立一个Holdout集，例如10%的训练数据，第二阶段的stacker模型就基于第一阶段模型对这10%训练数据的预测值进行拟合。说白了，就是把Stacking流程中的K-Fold CV 改成 HoldOut CV。如图所示。

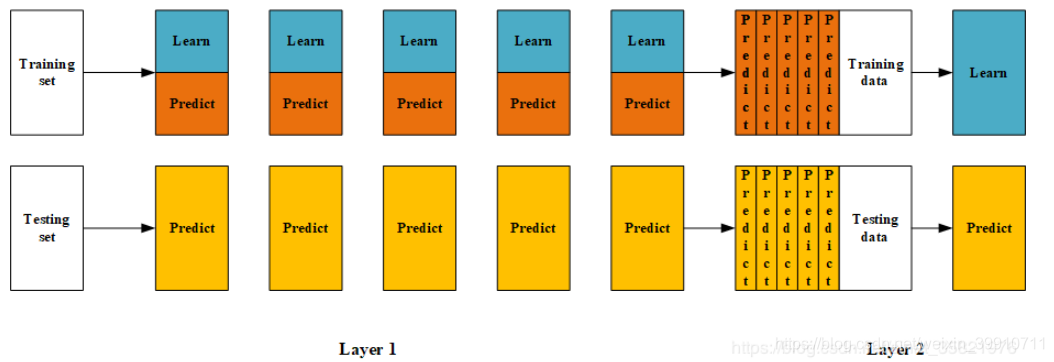
        Blending相较于Stacking来说要简单一些，其流程大致分为以下几步：

1. 将数据划分为训练集和测试集(test_set)，其中训练集需要再次划分为训练集(train_set)和验证集(val_set)；
2. 创建第一层的多个模型，这些模型可以使同质的也可以是异质的；
3. 使用train_set训练步骤2中的多个模型，然后用训练好的模型预测val_set和test_set得到val_predict, test_predict1；
4. 创建第二层的模型,使用val_predict作为训练集训练第二层的模型；
5. 使用第二层训练好的模型对第二层测试集test_predict1进行预测，该结果为整个测试集的结果。

2.5 方法对比

2.5.1 Bagging，Boosting的主要区别

1. 样本选择上：Bagging采用的是Bootstrap随机有放回抽样；而Boosting每一轮的训练集是不变的，改变的只是每一个样本的权重。
2. 样本权重：Bagging使用的是均匀取样，每个样本权重相等；Boosting根据错误率调整样本权重，错误率越大的样本权重越大，而权值是根据上一轮的分类结果进行调整。
3. 预测函数：Bagging所有的预测函数的权重相等；Boosting中误差越小的预测函数其权重越大，即每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。
4. 并行计算：Bagging各个预测函数可以并行生成；Boosting各个预测函数必须按顺序迭代生成，因为后一个模型参数需要前一轮模型的结果。

下面是将决策树与这些算法框架进行结合所得到的新的算法：

1）Bagging + 决策树 = 随机森林（Random Forest）

2）AdaBoost + 决策树 = 提升树（Boosting Decision Tree）

3）Gradient Boosting + 决策树 = 梯度提升树（Gradient Boosting Decision Tree，GBDT）

从方差-偏差角度分析 bagging 和 boosting：

• bagging 是并行的（即分别训练几个不同的模型，然后让所有模型表决测试样例的输出），每个基学习器可以单独训练。基学习器独立性很强，所以说 bagging 关注的是降低方差。
• boosting 是串行的，后一个学习器要在前一个学习器训练好之后才能训练，即学习器之间独立性没那么强，且 boosting 关注偏差 （每一步都会在上一轮的基础上更加的拟合原数据，所以可以保证偏差，所以对于每个基分类器来说，问题就是如何选择方差更小的分类器，即更简单的弱分类器）。于是 boosting 对样本集会拟合的更好，所以说boosting 关注的是降低偏差。

2.5.2 Blending与Stacking对比

Blending的优点：

1. 比stacking简单（因为不用进行k次的交叉验证来获得stacker feature）
2. 避开了一个信息泄露问题：generlizers和stacker使用了不一样的数据集
3. 在团队建模过程中，不需要给队友分享自己的随机种子

缺点：

1. 使用了很少的数据（是划分hold-out作为测试集，并非cv）
2. blender可能会过拟合（其实大概率是第一点导致的）
3. stacking使用多次的CV会比较稳健

3 常见问题

3.1 常用的基分类器是什么？

        最常用的基分类器是决策树， 主要有以下3个方面的原因。
（1） 决策树可以较为方便地将样本的权重整合到训练过程中， 而不需要使用过采样的方法来调整样本权重。
（2） 决策树的表达能力和泛化能力， 可以通过调节树的层数来做折中。
（3） 数据样本的扰动对于决策树的影响较大， 因此不同子样本集合生成的决策树基分类器随机性较大， 这样的“不稳定学习器”更适合作为基分类器。 此外，在决策树节点分裂的时候， 随机地选择一个特征子集， 从中找出最优分裂属性，很好地引入了随机性。  

        除了决策树外， 神经网络模型也适合作为基分类器， 主要由于神经网络模型也比较“不稳定”， 而且还可以通过调整神经元数量、 连接方式、 网络层数、 初始权值等方式引入随机性。

3.2 可否将随机森林中的基分类器， 由决策树替换为线性分类器或K-近邻？ 请解释为什么？

        随机森林属于Bagging类的集成学习。 Bagging的主要好处是集成后的分类器的方差， 比基分类器的方差小。 Bagging所采用的基分类器， 最好是本身对样本分布较为敏感的（即所谓不稳定的分类器） ， 这样Bagging才能有用武之地。 线性分类器或者K-近邻都是较为稳定的分类器， 本身方差就不大， 所以以它们为基分类器使用Bagging并不能在原有基分类器的基础上获得更好的表现， 甚至可能因为Bagging的采样， 而导致他们在训练中更难收敛， 从而增大了集成分类器的偏差。

3.3 如何从减小方差和偏差的角度解释Boosting和Bagging的原理？

       简单回答这个问题就是： Bagging能够提高弱分类器性能的原因是降低了方差， Boosting能够提升弱分类器性能的原因是降低了偏差。 为什么这么讲呢？

3.3.1  Bagging降低了方差

        首先， Bagging 是 Bootstrap Aggregating 的简称， 意思就是再抽样， 然后在每个样本上训练出来的模型取平均。

        假设有n个随机变量， 方差记为σ2， 两两变量之间的相关性为ρ， 则n个随机变量的均值的方差为 。 在随机变量完全独立的情况下， n个随机变量的方差为， 也就是说方差减小到了原来的1/n。

 样本是独立同分布时，为什么说样本均值的方法等于总体方差的n分之一？

独立同分布：

 有相关性：

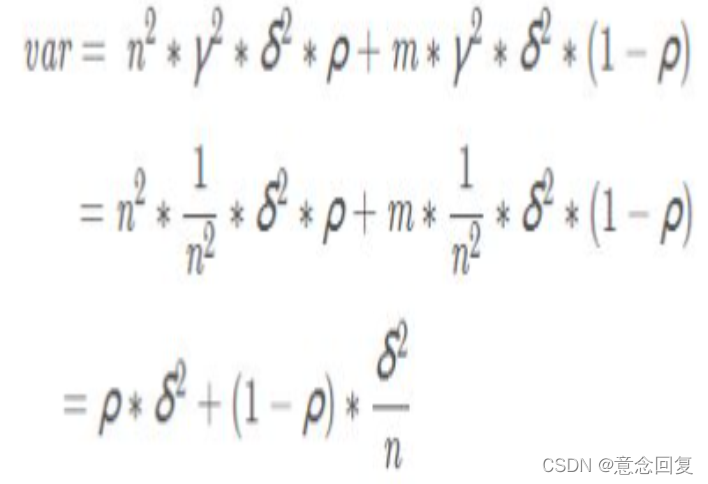
        再从模型的角度理解这个问题， 对n个独立不相关的模型的预测结果取平均，方差是原来单个模型的1/n。 这个描述不甚严谨， 但原理已经讲得很清楚了。 当然， 模型之间不可能完全独立。 为了追求模型的独立性， 诸多Bagging的方法做了不同的改进。 比如在随机森林算法中， 每次选取节点分裂属性时， 会随机抽取一个属性子集， 而不是从所有属性中选取最优属性， 这就是为了避免弱分类器之间过强的相关性。 通过训练集的重采样也能够带来弱分类器之间的一定独立性， 从而降低Bagging后模型的方差。

3.3.2 Boosting 降低了偏差

        大家应该还记得Boosting的训练过程。 在训练好一个弱分类器后， 我们需要计算弱分类器的错误或者残差， 作为下一个分类器的输入。 这个过程本身就是在不断减小损失函数， 来使模型不断逼近“靶心”， 使得模型偏差不断降低。 但Boosting的过程并不会显著降低方差。 这是因为Boosting的训练过程使得各弱分类器之间是强相关的， 缺乏独立性， 所以并不会对降低方差有作用。 

简单易学的机器学习算法——集成方法(Ensemble Method)_null的专栏-优快云博客_ensemble method

随机森林算法学习(RandomForest)_Eason的博客-优快云博客_随机森林算法

机器学习--集成学习（Ensemble Learning） - 理想几岁 - 博客园

GBDT基本原理及算法描述GBDT基本原理及算法描述_Y学习使我快乐V的博客-优快云博客_gbdt算法

AdaBoost基本原理与算法描述： AdaBoost基本原理与算法描述_Y学习使我快乐V的博客-优快云博客_adaboost

XGBoost的基本原理：XGBoost的基本原理_Y学习使我快乐V的博客-优快云博客_xgboost原理