求一段乱七八糟的乱码_【国际数学竞赛】递推数列求极限(1)

国际数学竞赛一般考除微积分以外所有高中数学知识，极限不仅是微积分的核心在竞赛中也时常出现，比如无穷等比数列的和

就经常和概率一起考，

另一种常见的考法就是给一个初始状态然后按照一定规律运动，问最后的状态是什么样子。碰到第二类题，我们可以借助数列进行求解，下面通过一道AMC试题进行讲解。

2019-AMC10B-18

题意：一天早上Henry出去锻炼，家与健身房相距2千米。当他从家到健身房走了

的路程时，他改变了主意决定掉头回家。但是，当他往家走了

路程时又改变了主意，又决定掉头去健身房。如果他一直在往家或者健身房路上走了

路程时改变注意，那么最后他会在两个固定点来回走。假设这两个点距离家分别为

千米和

千米，请问

等于多少？

因为从家往健身房和从健身房往家有两个转折点，那么这里我们设两个数列，设从家往健身房走，改变主意时该点距离家的距离为

;设从健身房往家走，改变主意的点距离家的距离为

。

根据题意，很容易知道，

;

。

接下去我们可以构建

与

之间的关系：

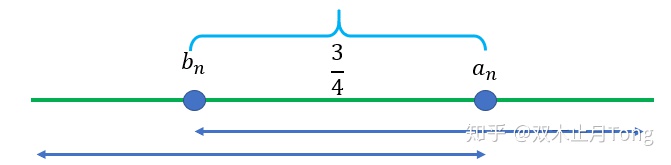
所以，

,

。这里我们就能把

求解出来。

设

,解得

,

因此，

,

。

那么当

趋于无穷时，

,于是

。

也就是

。

到这里我们就把题目完全解决了，通过设两个数列，找到它们之间的数量关系，然后就把问题转变成了一个单纯的数列求解问题，而型如

的数列也是非常经典的一类递推数列。

这一题我们也有更加简单的方法来求解。

图：O为家，E为健身房，AB为转折点

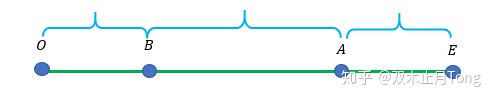
不妨设经过很长时间后Henry在AB两点间来回走。

根据题意可知，Henry从B点出发往E走，A点是转折点，那么

,

所以，

。

而Henry从A点往O点走时，B点是转折点，那么

，

所以，

。

结合上述两式可知，

，

因此

。

法二是从平衡位置出发进行分析这也是常用的方法与技巧。

这一题是构建了

与

两个数列之间的关系，那么有时我们还会建立起三个数列之间的关系，可以参阅下文：

双木止月Tong：【国际数学竞赛】递推数列求极限(2)​zhuanlan.zhihu.com

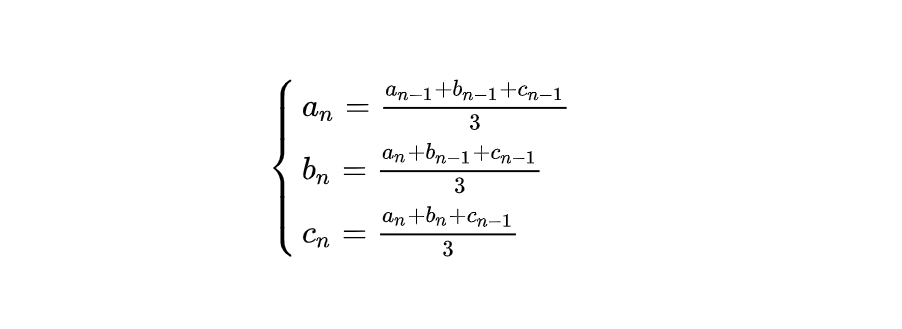
一己拙见，欢迎大家交流讨论，希望大家点赞支持~~

如果想了解更多国际数学竞赛真题，可参阅下文：

双木止月Tong：【国际数学竞赛】目录​zhuanlan.zhihu.com