c++八股文整理（九）

1. STL中unordered_map和map的区别和应用场景

map支持键值的自动排序，底层机制是红黑树，红黑树的查询和维护时间复杂度均为$O(logn)$，但是空间占用比较大，因为每个节点要保持父节点、孩子节点及颜色的信息

unordered_map是C++ 11新添加的容器，底层机制是哈希表，通过hash函数计算元素位置，其查询时间复杂度为O(1)，维护时间与bucket桶所维护的list长度有关，但是建立hash表耗时较大

从两者的底层机制和特点可以看出：map适用于有序数据的应用场景，unordered_map适用于高效查询的应用场景

2. 红黑树概念

1、它是二叉排序树（继承二叉排序树特显）：

• 若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值。
• 若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值。
• 左、右子树也分别为二叉排序树。

2、它满足如下几点要求：

• 树中所有节点非红即黑。
• 根节点必为黑节点。
• 红节点的子节点必为黑（黑节点子节点可为黑）。
• 从根到NULL的任何路径上黑结点数相同。

3、查找时间一定可以控制在O(logn)

3. STL中的priority_queue的实现

priority_queue，优先队列，是一个拥有权值观念的queue，它跟queue一样是顶部入口，底部出口，在插入元素时，元素并非按照插入次序排列，它会自动根据权值（通常是元素的实值）排列，权值最高，排在最前面，如下图所示。

默认情况下，priority_queue使用一个max-heap完成，底层容器使用的是一般为vector为底层容器，堆heap为处理规则来管理底层容器实现 。priority_queue的这种实现机制导致其不被归为容器，而是一种容器配接器。关键的源码如下：

template <class T, class Squence = vector<T>, 
class Compare = less<typename Sequence::value_tyoe> >
class priority_queue{
	...
protected:
    Sequence c; // 底层容器
    Compare comp; // 元素大小比较标准
public:
    bool empty() const {return c.empty();}
    size_type size() const {return c.size();}
    const_reference top() const {return c.front()}
    void push(const value_type& x)
    {
        c.push_heap(x);
        push_heap(c.begin(), c.end(),comp);
    }
    void pop()
    {
        pop_heap(c.begin(), c.end(),comp);
        c.pop_back();
    }
};

priority_queue的所有元素，进出都有一定的规则，只有queue顶端的元素（权值最高者），才有机会被外界取用，它没有遍历功能，也不提供迭代器

举个例子：

#include <queue>
#include <iostream>
using namespace std;

int main()
{
	int ia[9] = {0,4,1,2,3,6,5,8,7 };
	priority_queue<int> pq(ia, ia + 9);
	cout << pq.size() <<endl;  // 9
	for(int i = 0; i < pq.size(); i++)
	{
		cout << pq.top() << " "; // 8 8 8 8 8 8 8 8 8
	}
	cout << endl;
	while (!pq.empty())
	{
		cout << pq.top() << ' ';// 8 7 6 5 4 3 2 1 0
		pq.pop();
	}
	return 0;
}

4. STL中的heap的实现

heap（堆）并不是STL的容器组件，是priority queue（优先队列）的底层实现机制，因为binary max heap（大根堆）总是最大值位于堆的根部，优先级最高。

binary heap本质是一种完全二叉树，整棵binary tree除了最底层的叶节点之外，都是填满的，叶节点从左到右不会出现空隙。

完全二叉树内没有任何节点漏洞，是非常紧凑的，这样的一个好处是可以使用array来存储所有的节点。因此我们可以使用一个array和一组heap算法来实现max heap（每个节点的值大于等于其子节点的值）和min heap（每个节点的值小于等于其子节点的值）。由于array不能动态的改变空间大小，所以用vector代替array。

push_heap插入算法

pop_heap算法 

sort算法

因为pop_heap可以将当前heap中的最大值置于底层容器vector的末尾，heap范围减1，那么不断的执行pop_heap直到树为空，即可得到一个递增序列。

make_heap算法

将一段数据转化为heap，一个一个数据插入，调用上面说的两种percolate算法即可。

代码实测：

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main()
{
	vector<int> v = { 0,1,2,3,4,5,6 };
	make_heap(v.begin(), v.end()); //以vector为底层容器
	for (auto i : v)
	{
		cout << i << " "; // 6 4 5 3 1 0 2
	}
	cout << endl;
	v.push_back(7);
	push_heap(v.begin(), v.end());
	for (auto i : v)
	{
		cout << i << " "; // 7 6 5 4 1 0 2 3
	}
	cout << endl;
	pop_heap(v.begin(), v.end());
	cout << v.back() << endl; // 7 
	v.pop_back();
	for (auto i : v)
	{
		cout << i << " "; // 6 4 5 3 1 0 2
	}
	cout << endl;
	sort_heap(v.begin(), v.end());
	for (auto i : v)
	{
		cout << i << " "; // 0 1 2 3 4 5 6
	}
	return 0;
}

5. STL中的deque的实现

vector是单向开口（尾部）的连续线性空间，deque则是一种双向开口的连续线性空间。

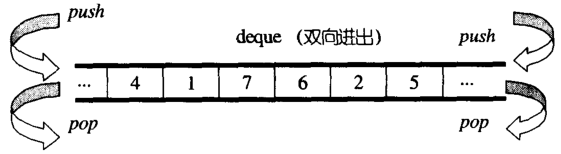
deque和vector的最大差异一个是deque运行在常数时间内对头端进行元素操作，二是deque没有容量的概念，它是动态地以分段连续空间组合而成，可以随时增加一段新的空间并链接起来

deque虽然也提供随机访问的迭代器，但是其迭代器并不是普通的指针，其复杂程度比vector高很多，因此除非必要，否则一般使用vector而非deque。如果需要对deque排序，可以先将deque中的元素复制到vector中，利用sort对vector排序，再将结果复制回deque

deque由一段一段的定量连续空间组成，一旦需要增加新的空间，只要配置一段定量连续空间拼接在头部或尾部即可，因此deque的最大任务是如何维护这个整体的连续性

 

deque的迭代器数据结构如下：

struct __deque_iterator
{
    ...
    T* cur;//迭代器所指缓冲区当前的元素
    T* first;//迭代器所指缓冲区第一个元素
    T* last;//迭代器所指缓冲区最后一个元素
    map_pointer node;//指向map中的node
    ...
}

从deque的迭代器数据结构可以看出，为了保持与容器联结，迭代器主要包含上述4个元素。

如果map中node数量全部使用完，且node指向的缓冲区也没有多余的空间，这时会配置新的map（2倍于当前+2的数量）来容纳更多的node，

6. STL中slist的实现

list是双向链表，而slist（single linked list）是单向链表，它们的主要区别在于：前者的迭代器是双向的Bidirectional iterator，后者的迭代器属于单向的Forward iterator。虽然slist的很多功能不如list灵活，但是其所耗用的空间更小，操作更快。

7. STL中迭代器失效的情况有哪些？

以vector为例：

插入元素：

1、尾后插入：size < capacity时，尾迭代失效（未重新分配空间），size == capacity时，所有迭代器均失效（需要重新分配空间）。

2、中间插入：中间插入：size < capacity时，首迭代器不失效但插入元素之后所有迭代器失效，size == capacity时，所有迭代器均失效。

删除元素：

尾后删除：只有尾迭代失效。

中间删除：删除位置之后所有迭代失效。

8. 说一下STL每种容器对应的迭代器

容器	迭代器
vector、deque	随机访问迭代器
stack、queue、priority_queue	无
list、(multi)set/map	双向迭代器
unordered_(multi)set/map、forward_list	前向迭代器