计算机组成五大部分数据通路,突破计算机组成原理面试：设计 CPU 数据通路（中）...

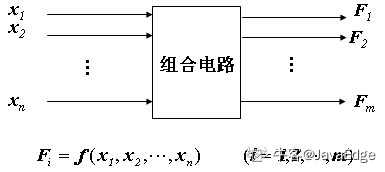
1 概述

1.1 组合逻辑电路(combinatorial logic或combinational logic Circuit)

只需要给定输入，就能得到固定的输出。这样的电路，即组合逻辑电路

但是，光有组合逻辑电路是不够的。如果只有组合逻辑电路, 电路输入是确定的，对应的输出自然也就确定了。

那么，我们要进行不同的计算，就要去手动拨动各种开关，来改变电路的开闭状态。这样的计算机，不像我们现在每天用的功能强大的电子计算机，

反倒更像古老的计算尺或者机械计算机，干不了太复杂的工作，只能协助我们完成一些计算工作。

在数字电路理论中，组合逻辑电路(combinatorial logic或combinational logic)是一种逻辑电路，它的任一时刻的稳态输出，仅仅与该时刻的输入变量的取值有关，而与该时刻以前的输入变量取值无关。相对于组合逻辑电路，时序逻辑电路的输出结果除了依照目前的输入外也和先前的输入有关系。从电路结构分析，组合电路由各种逻辑门组成，网络中无记忆元件，也无反馈线。

组合逻辑是在电脑被用来做输入的信号跟储存的资料作逻辑代数运算之用。实际上电脑电路都会混用包含组合逻辑和时序逻辑的电路。举例来说，算术运算逻辑单元(ALU)中，尽管ALU是由循序逻辑的程序装置所控制，而数学的运算就是从组合逻辑制产生的。计算机中用到的其他电路，如半加器、全加器、半减器、全减器、数据选择器、数据分配器、编码器和译码器也用来构成组合逻辑电路。

1.2 痛点的解决方案 - 时序逻辑(Sequential Logic Circuit)

需要引入第二类的电路，也就是时序逻辑电路,

在数字电路理论中，时序逻辑电路是指电路任何时刻的稳态输出不仅取决于当前的输入，还与前一时刻输入形成的状态有关。

这跟组合逻辑电路相反，组合逻辑的输出只会跟目前的输入成一种函数关系。换句话说，时序逻辑拥有储存元件(内存)来存储信息，而组合逻辑则没有。

可以帮我们解决这样几个痛点

1.2.1 自动运行

时序电路接通之后可以不停地开启和关闭开关，进入一个自动运行的状态

这使得控制器不停地让PC寄存器自增读取下一条指令成为可能!

1.2.2 存储

通过时序电路实现的触发器，能把计算结果存储在特定的电路里面

而不是像组合逻辑电路那样，一旦输入有任何改变，对应的输出也会改变。

1.2.3 时序协调

本质上解决了各个功能按照时序协调的问题

无论是程序实现的软件指令，还是到硬件层面，各种指令的操作都有先后的顺序要求。

时序电路使得不同的事件按照时间顺序发生!

2 时钟信号的硬件实现

那么想要实现SLC，第一步我们需要的就是一个时钟

CPU的主频是由一个晶体振荡器来实现的，而这个晶体振荡器生成的电路信号，就是我们的时钟信号

实现这样一个电路，和通过电的磁效应产生开关信号的方法是一样的。只不过，这里的磁性开关，打开的不再是后续的线路，而是当前的线路。

时钟信号

如下图, 在一般只放一个开关的信号输入端，放上了两个开关

开关A，一开始是断开的，手工控制

开关B，一开始是合上的，磁性线圈对准一开始就合上的开关B

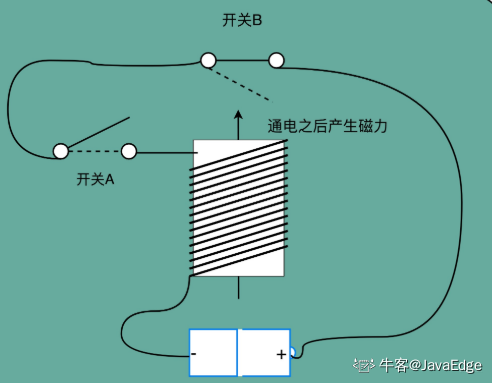
于是，一旦合上开关A，磁性线圈就会通电，产生磁性，开关B就会从合上变成断开

一旦这个开关断开，电路就中断了，磁性线圈就失去了磁性。于是，开关B又会弹回到合上的状态。

这样一来，电路接通，线圈又有了磁性。我们的电路就会来回不断地在开启、关闭这两个状态中切换。

这个不断切换的过程，对于下游电路来说，就是不断地产生新的0和1这样的信号。

如果你在下游的电路上接上一个灯泡，就会发现这个灯泡在亮和暗之间不停切换。

这个按照固定的周期不断在0和1之间切换的信号，就是我们的时钟信号(Clock Signal)。

反馈电路(Feedback Circuit)

一个振荡产生的0、1信号

这种电路，就相当于把电路的输出信号作为输入信号，再回到当前电路, 这样的电路构造方式叫作 反馈电路

接下来，我们还会看到更多的反馈电路

上面这个反馈电路一般可以用下面这个示意图来表示，其实就是一个输出结果接回输入的反相器(Inverter)，也就是非门

3 通过D触发器实现存储功能

3.1 有记忆功能的电路

有了时钟信号，我们的系统里就有了一个像“自动门”一样的开关。

利用这个开关和相同的反馈电路，就可以构造出一个有“记忆”功能的电路。

这个有记忆功能的电路可以实现,

在CPU中用来存储计算结果的寄存器

计算机五大组成部分之一的存储器

看下面这个RS触发器电路, 这个电路由两个或非门电路组成, 在图里面，把它标成了A和B

在这个电路一开始，输入开关都是关闭的，所以或非门(NOR)A的输入是0和0

对应到真值表，输出就是1

而或非门B的输入是0和A的输出1

对应输出就是0。B的输出0反馈到A，和之前的输入没有变化，A的输出仍然是1。而整个电路的 输出Q，也就是0。

当我们把A前面的开关R合上的时候，A的输入变成了1和0，输出就变成了0，对应B的输入变成0和0，输出就变成了1。B的输出1反馈给到了A，A的输入变成了1和1，

输出仍然是0。所以把A的开关合上之后，电路仍然是稳定的，不会像晶振那样振荡，但是整个电路的 输出Q变成了1。

这个时候，如果我们再把A前面的开关R打开，A的输入变成和1和0，输出还是0，对应的B的输入没有变化，输出也还是1。B的输出1反馈给到了A，A的输入变成了1和0，输出仍然是0。这个时候，电路仍然稳定。 开关R和S的状态和上面的第一步是一样的，但是最终的输出Q仍然是1，和第1步里Q状态是相反的。我们的输入和刚才第二步的开关状态不一样，但是输出结果仍然保留在了第2步时的输出没有发生变化。

这个时候，只有我们再去关闭下面的开关S，才可以看到，这个时候，B有一个输入必然是1，所以B的输出必然是0，也就是电路的最终 输出Q必然是0。

3.2 触发器

这样一个电路，我们称之为触发器(Flip-Flop)。

接通开关R，输出变为1，即使断开开关，输出还是1不变

接通开关S，输出变为0，即使断开开关，输出也还是0

即, 当两个开关都断开，最终输出结果，取决于之前动作的输出结果，这个也就是我们说的记忆功能。

这里的这个电路是最简单的RS触发器，也就是所谓的复位置位触发器(Reset-Set Flip Flop)

对应的输出结果的真值表

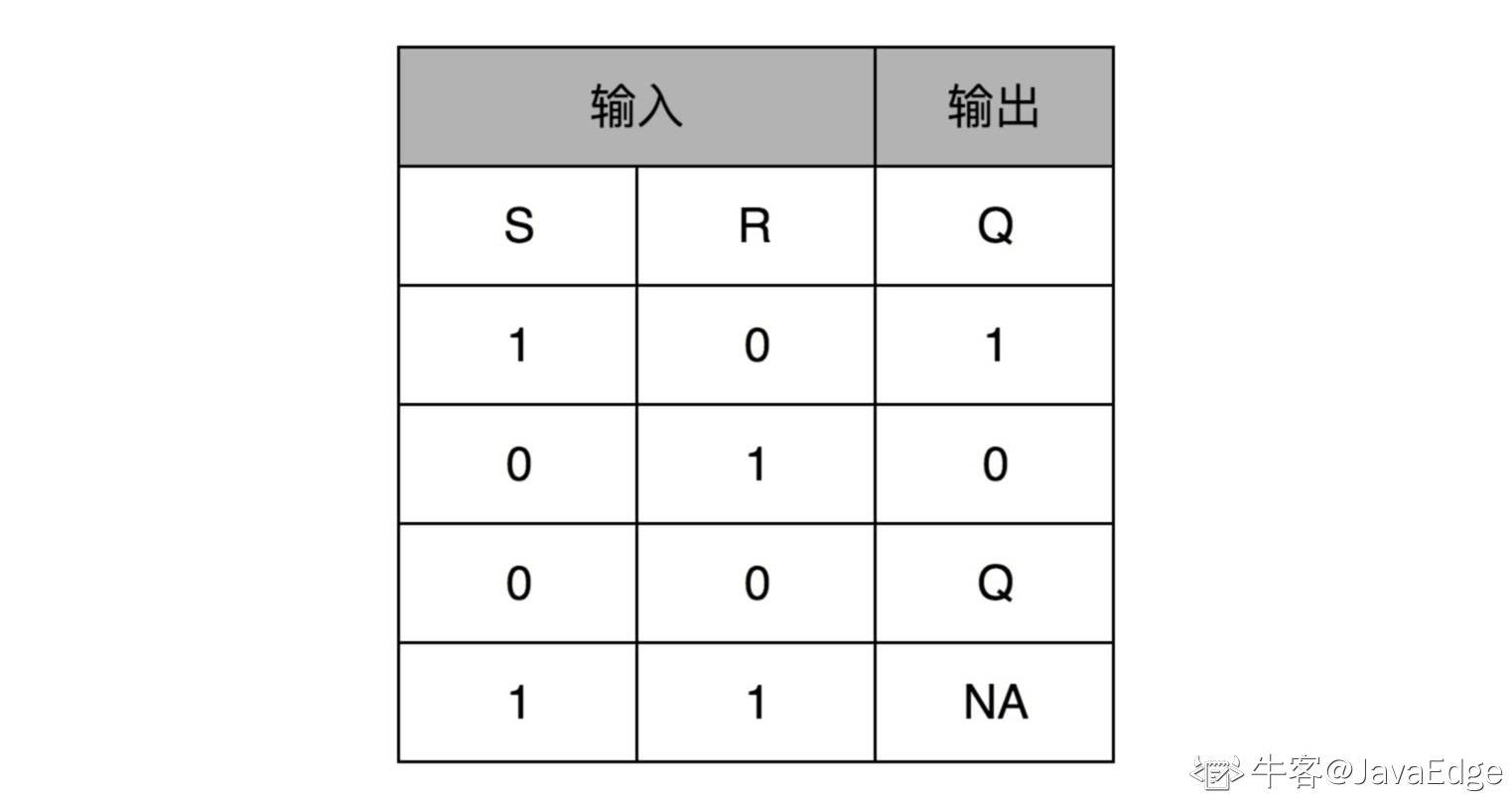
当两个开关都是0，对应的输出是和Q的上一个状态一致

再往这个电路里加两个与门和一个时钟信号，我们就可以实现一个利用时钟信号来操作一个电路了。这个电路可以帮我们实现什么时候可以往Q里写入数据

我们看看下面这个电路

在R-S触发器基础之上，在R和S开关之后

加入了两个与门

这两个与门加入了一个时钟信号CLK作为电路输入

这样，当时钟信号CLK在低电平，与门输入里有一个0，两个实际的R和S后的与门的输出必然是0

无论怎么按R和S的开关，根据真值表，对应的Q输出都不会发生变化

只有当时钟信号CLK在高电平，与门的一个 输入是1，输出结果完全取决于R和S的开关。我们可以在这个时候，通过开关R和S，来决定对应Q的输出。

如果这个时候，让R和S的开关，也用一个反相器

反相器(英语：Inverter)也称非门(英语：NOT gate)，是数字逻辑中实现逻辑非的逻辑门

连起来，也就是通过同一个开关控制R和S

只要CLK信号是1，R和S就可以设置输出Q

当CLK信号是0时，无论R和S怎么设置，输出信号Q是不变的

这样就成了最常用的D型触发器

用来控制R和S这两个开关的信号，视作一个输入的数据信号D，也就是Data，这就是D型触发器的由来!

一个D型触发器，只能控制1个比特的读写

但是如果我们同时拿出多个D型触发器并列在一起

并且把用同一个CLK信号控制作为所有D型触发器的开关

这就变成了一个N位的D型触发器，也就可以同时控制N位的读写!

CPU里面的寄存器可以直接通过D型触发器来构造

可以在D型触发器的基础上，加上更多的开关，来实现清0或者全部置为1这样的快捷操作!

4 总结

通过引入了时序电路，实现了数据“存储”

通过反馈电路，创建了时钟信号，然后再利用这个时钟信号和门电路组合，实现了“状态记忆”的功能。

电路的输出信号不单单取决于当前的输入信号，还要取决于输出信号之前的状态。

最常见就是D触发器，它也是实际在CPU内实现存储功能的寄存器的实现方式。

这也是现代计算机体系结构中的“冯·诺伊曼”机的一个关键，就是程序需要可以“存储”，而不是靠固定的线路连接或者手工拨动开关，来实现计算机的可存储和可编程的功能。

有了时钟信号和触发器之后，我们还差一个“自动”需求没有实现

我们的计算机还不能做到自动地不停地从内存里面读取指令去执行。

请见下文分解

参考