蒙特卡洛模拟_蒙特卡洛模拟方法及应用案例

蒙特卡罗法也称统计模拟法、统计试验法。是把概率现象作为研究对象的数值模拟方法。是按抽样调查法求取统计值来推定未知特性量的计算方法。蒙特卡罗法作为一种计算方法，是由美国数学家乌拉姆与美籍匈牙利数学家冯·诺伊曼在20世纪40年代中叶，为研制核武器的需要而首先提出来的。蒙特卡罗是摩纳哥的著名赌城，该法为表明其随机抽样的本质而命名，故适用于对离散系统进行计算仿真试验。在计算仿真中，通过构造一个和系统性能相近似的概率模型，并在数字计算机上进行随机试验，可以模拟系统的随机特性。

蒙特卡洛法是描述装备运用过程中各种随机现象的基本方法，而且它特别适用于一些解析法难以求解甚至不可能求解的问题，因而在装备效能评估中具有重要地位。

蒙特卡洛法的基本思想是：为了求解问题，首先建立一个概率模型或随机过程，使它的参数或数字特征等于问题的解；然后通过对模型或过程的观察或抽样试验来计算这些参数或数字特征，最后给出所求解的近似值。解的精确度用估计值的标准误差来表示。蒙特卡洛法的主要理论基础是概率统计理论，主要手段是随机抽样、统计试验。

用蒙特卡洛法求解实际问题的基本步骤为：

01 根据实际问题的特点，构造简单而又便于实现的概率统计模型，使所求的解恰好是所求问题的概率分布或数学期望；

02 给出模型中各种不同分布随机变量的抽样方法；

03 统计处理模拟结果，给出问题解的统计估计值和精度估计值。

    给一个蒙特卡洛解题案例，现有如下问题：求解曲线y1，y2所围区域的面积，给出近似解即可？

x=-5:0.05:5;y1=x.^3.3+x.^2.4-20*x.^(4/3);y2=x.^(sqrt(5))+5;

    两曲线方程虽然阶次不高，但很是复杂，用解析法颇有难度，对不擅长数学的人来说甚至不可求解，亦不太可能给出近似解。

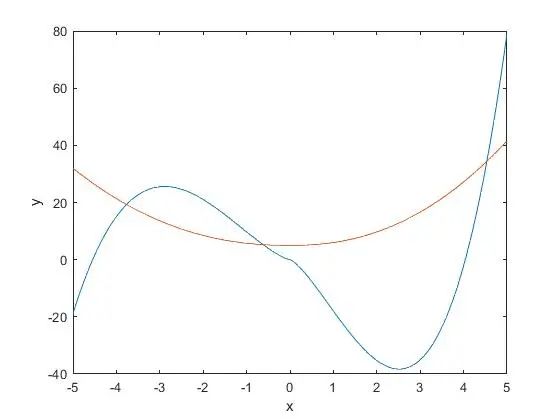
下面以蒙特卡洛模拟给出解决思路：

01 在x=[-5,5]，y=[-40,80]范围内生成均匀分布的随机点；

02 计算曲线y1，y2所围区域内的点数；

03 符合02中的点数在总点数中的占比；

04 上述比例乘以面积1200(矩形面积)，即得到该题近似解。

矩形区间随机点的分布如下，基本上属于均匀分布。

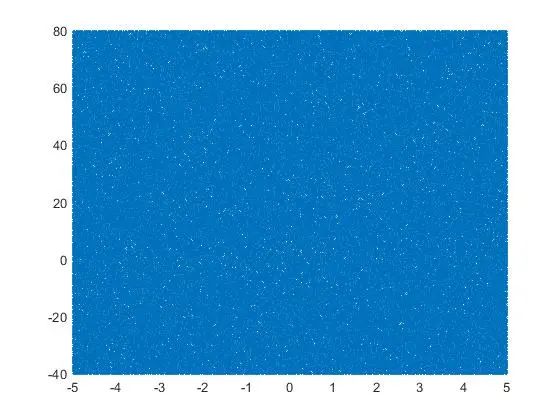
符合曲线所围区间的点如下：

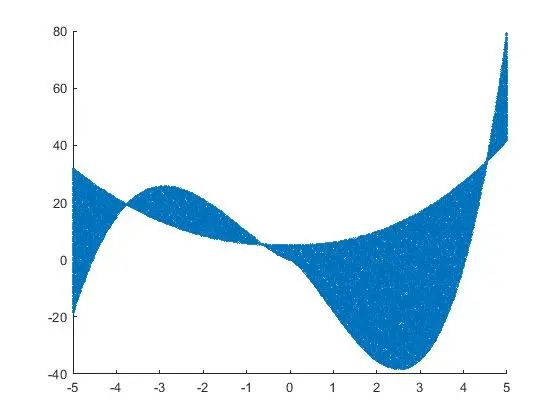
求解得到，占比约0.1795，面积约215.4266.

求解精度与样本点数关系如下：

样本点数从1000到5千万(受限于计算机性能)，每级样本数重复3次试验，可以看到3次试验中最大值与最小值的差异在逐渐减小，即模拟结果趋于收敛，离散点数达到5千万级别时，近似误差可达到万分之一级别。

蒙特卡洛法广泛应用于可靠性、鲁棒性、6sigma等工程领域，亦于统计学、社会学、博弈论、金融、军事等领域发挥了重要作用。

[历史文章]

WLTC尺度缩减修正路谱APP开发

WLTC尺度缩减修正路谱

AVL Random Cycle Generator随机路谱生成器

Matlab “for”循环的运行效率及优化探究

Tensorboard网络结构及可视化

Tensorflow在Windows环境搭建方法

Isight混合优化策略方法与实践

Isight-Simulink联合仿真方法实践

近似模型之响应面建模

近似模型之响应面建模|02