拉格朗日乘子_Calculus Review 14.8 拉格朗日乘子法

^[1]拉格朗日乘子是一种用来找到限制条件下函数的最值的方法。

受约束的^[2]最大值与最小值

例题1
求平面

上离原点最近的点。

　　这个很简单，就是把

代入

，转化为二元函数，再利用之前的知识求解就行。但是代换法并不是每次都能使用得很smooth.

　　另一个例子则能很好说明代换法的局限性。

例题2
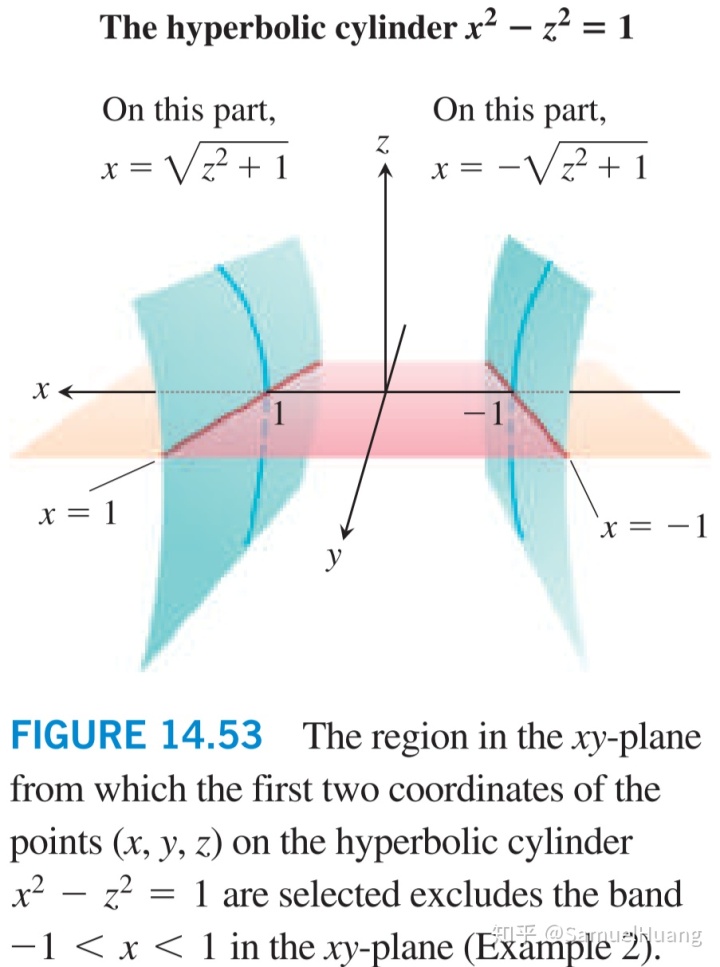
求hyperbolic cylinder

上离原点最近的点。

　　如果采用代换法，将

代入

中，得到

，要求最小值，就有

　　也就是原点本身，这个答案肯定很滑稽。之所以会这样，是因为我们需要的点是是在hyperbolic cylinder上的，而代换之后找目标点是以整个

平面为范围的。

错误的定义域

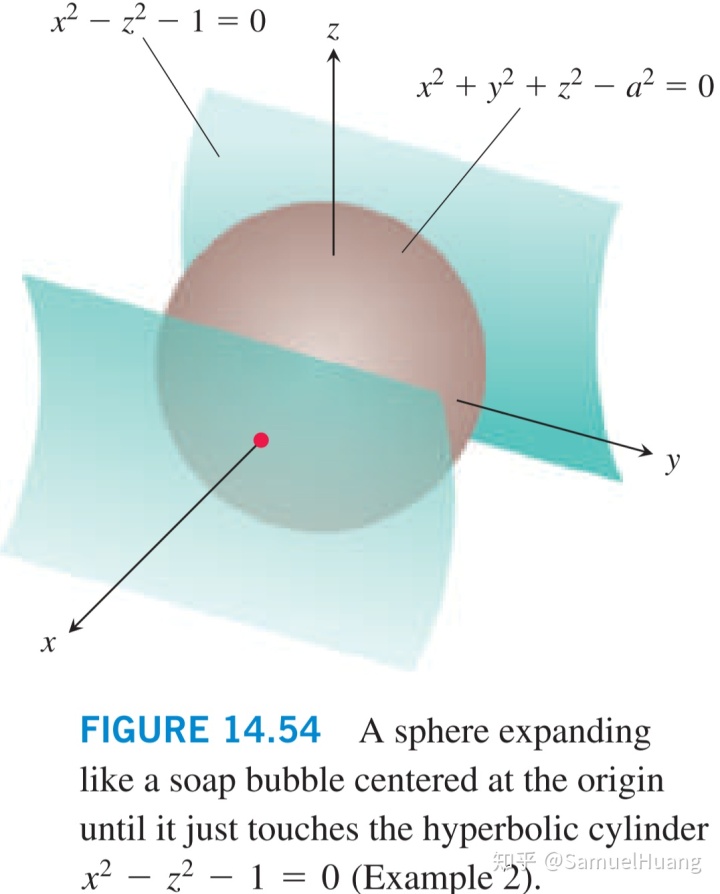
　　能够避开对于范围的讨论而得到结果的另一种方法，则是考虑一个以原点为球心，

为半径的“泡泡”。这个“泡泡”不断地变大，它刚好碰到hyperbolic cylinder的时候，那个交点肯定就是到原点距离最小的点，距离为

。

　　“泡泡”与hyperbolic cylinder的方程分别为：

　　临界条件是它们相切，也就是切平面方向平行，也就是法线方向平行，也就是梯度向量平行……也就是：

　　也就是

　　显然

，所以

，

。回带进限制方程

，得到

。

REMARK：以上即为使用拉格朗日乘子法的一般形式

拉格朗日乘子法的“泡泡”

拉格朗日乘子法

　　利用上面这个式子找到最值点的方法，就叫拉格朗日乘子法，

称为

拉格朗日乘子。

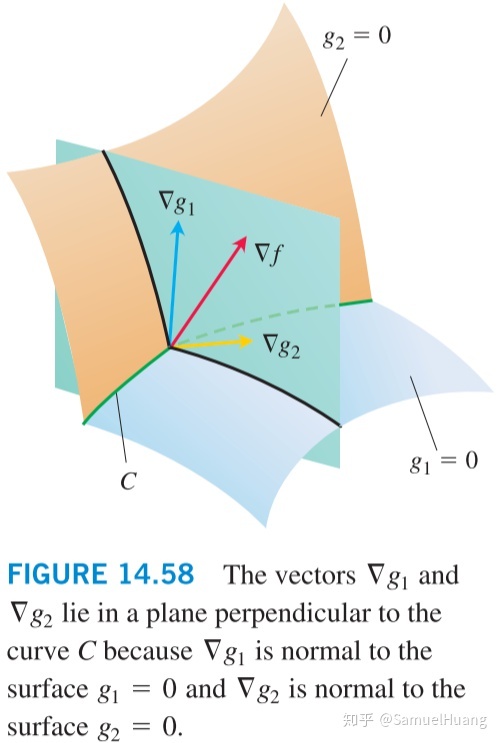
定理12：正交梯度定理
假设

在区域上可微，在其内部有光滑曲线

若

在

上一点

处取得局域最大值或最小值，则

在

处正交于

。

原因是

　　　定理12是拉格朗日乘子法的关键所在。

拉格朗日乘子法

和

可微且当

时

。要找到

受限制与

的区域最大值、最小值，需要找到

同时满足

双重限制的拉格朗日乘子

　　有的问题要求有更多的限制，可以引入两个拉格朗日乘子。

有两重限制的拉格朗日乘子法

　　从几何上解释，根据定理12，要找到的是正交于

的

。由于

位于

与

上，而梯度向量与平面是正交的，所以

与

也与

正交。这样，通过把

表示为

和

的线性组合，就达到了目的。

REMARK：这个地方有点tricky，一开始我还真没怎么想清楚到底是怎么回事。

---

REMARK：概括拉格朗日乘子法的使用

• 找到限制条件，表示为某函数等于0的形式
• 找到目标函数，表示为一个三元函数
• 分别求出梯度向量，列等式
• 将结果回带进限制条件，解出坐标
• 最后记得检验结论是否合理正确

　　这节的内容听起来很好像简单，但是真正做题的时候可能是另一回事，并且每个定理和每个推导的背后都有很强的逻辑性。感谢写这篇文章让我认真把这些问题考虑清楚ヾ(^▽^*)))

参考

1. ^Lagrange Multipliers
2. ^Constrained