泊松分布样本均值的数学期望_抽样分布

一、统计量

样本均值：从总体中抽样的数据集叫样本。样本总和除以样本总数即为样本均值。

样本方差：样本与样本均值之差的平方的和，除以（样本总数-1）。

样本变异系数：样本标准差与样本均值之比，是在消除量纲影响后的样本分散程度的一种度量。

样本K阶矩：专业术语应该为样本K阶原点矩，样本K次方的和的均值。

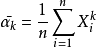
样本K阶中心矩：(样本减去样本均值)的K次方的和的均值。

样本偏度：样本偏度是样本3阶中心矩除以（样本2阶中心矩的3/2次幂)的商，记为Sk。样本偏度常用作总体偏度的估计量和检验总体分布正态性的统计量。

样本峰度：样本4阶中心矩除以（样本2阶中心矩平方）的商再减去3，记为Ku。样本峰度常用以作总体峰度的估计量，正态分布的峰度为0，非正态分布的峰度是以正态分布的峰度为标准来描述其分布密度形状为陡峭或平坦的一个数字特征。

次序统计量：设 X1,X2, …, Xn是取自总体X的样本，X(i) 称为该样本的第i个次序统计量，它的取值是将样本观测值由小到大排列后得到的第i个观测值。从小到大排序为x(1),x(2), …,x(n)，则称X(1),X(2), …,X(n)为顺序统计量。

充分统计量：对于给定的统计推断问题，包含了原样本中关于该问题的全部有用信息的统计量。对于未知参数的估计问题，保留了原始样本中关于未知参数θ的全部信息的统计量，就是充分统计量。如样本均值X是总体数学期望的充分统计量。数学上，设(X₁， …，Xₑ)是来自总体X的一个随机样本，T=T(X₁， …，Xₑ)是一统计量。若在T=t的条件下，样本的条件分布与未知参数θ无关，则称统计量T是θ的充分统计量。样本中包含关于总体的信息可分为两部分：其一是关于总体结构的信息，即反映总体分布的结构；其二是关于总体中未知参数的信息，这是由于样本的分布中包含了总体分布中的未知信息。我们对信息的加工只会减少，不会增多，即统计量具有压缩数据功能，但会凸显我们需要的信息。那么一个好的统计量应该能将样本中包含未知参数的全部信息提取出来，即样本加工不损失未知参数的信息称为充分性。

二、抽样分布

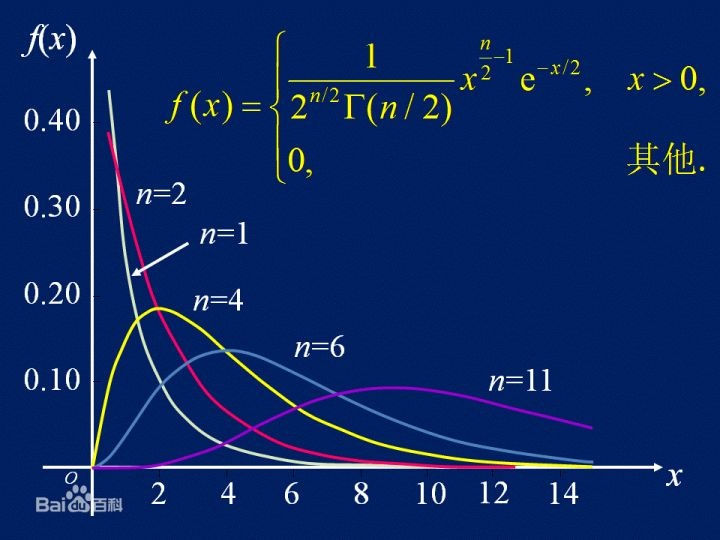
卡方分布：若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布，则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布(chi-square distribution)。

T分布：即学生t-分布，用于根据小样本（样本数小于30）来估计呈正态分布且方差未知的总体的均值。

F分布：若总体X~N(0,1)，（X1,X2,……Xn1）与（Y1,Y2,……Yn2）为来自X的两个独立样本，设统计量

则称统计量F服从自由度n1和n2的F分布，记为F~F(n1,n2)。

样本方差的分布：

样本比例的抽样分布：

大样本时比例分布逼近正态分布

中心极限定理：

两个样本平均值之差的分布：

两样本方差之比的分布：