逻辑回归算法_逻辑回归是分类算法or回归算法？女算法工程师教你如何解逻辑回归...

我的视频：跟 女算法工程师 学习 线性回归 与 逻辑回归

视频地址：https://www.ixigua.com/i6704826319307276808/

基于上一篇讲解线性回归的算法，这一篇将讲解逻辑回归算法的求解过程，首先声明一下，所有的公式我不进行展开推导，我只列原始公式，推导的部分希望大家可以自己完成啦。

言归正传，开始话说逻辑回归，逻辑回归是一个分类模型，记住是分类模型啊，这里再次强调一下，是分类分类分类模型！！！其思想也是基于线性回归，属于广义线性回归模型，其公式为

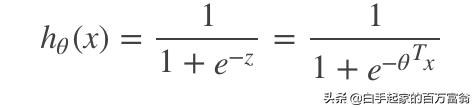
其中

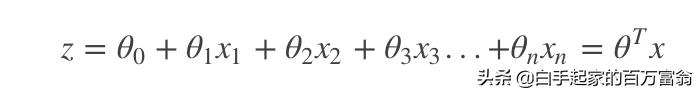
那如果仔细观察的朋友就会发现，z其实就是我上一期讲的线性回归的预测函数了，那这样我们就可以把逻辑回归的公式拆开来看，一个是

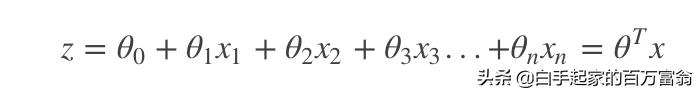
还有一个是

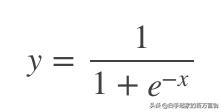
那y这个函数是什么呢，其实就是机器学习中非常常用的sigmoid函数了，下图展示的是sigmoid函数的图像

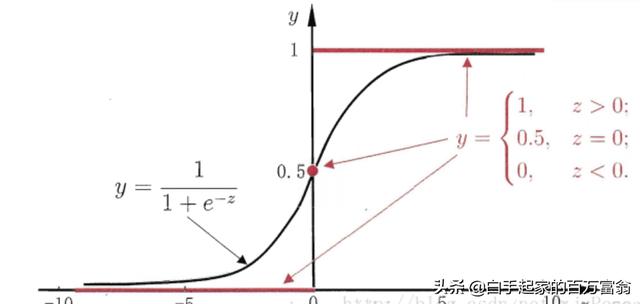
这是一个非常优美的函数图像啊，那把函数拆开来看，我们就很容易理解逻辑回归算法了，其实就是将线性回归的结果映射到sigmoid函数上，当sigmoid函数值大于0.5的时候，判断为正类，反之，则判断为负类，所以说逻辑回归不是回归算法，而是分类算法，说到这，我们已经了解了逻辑回归算法的思想，那接下来就是如何求解了，和线性回归算法类似，也是三个步骤

1.预测函数

和线性回归一样，需要先找到一个预测函数(h)，因为这是一个分类算法，因此输出值是两个值，所以利用了sigmoid函数，如下两个图的数据划分边界，一个是线性边界

一个是非线性边界

这里先只讲解线性边界，对于线性边界，其描述为

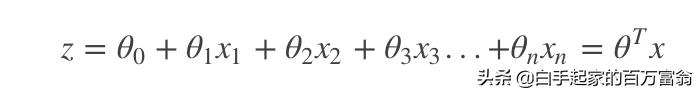
套上sigmoid函数，构造预测函数为

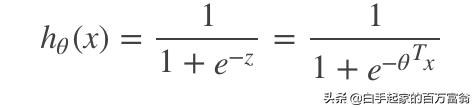
hθ(x)函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1的概率分别为

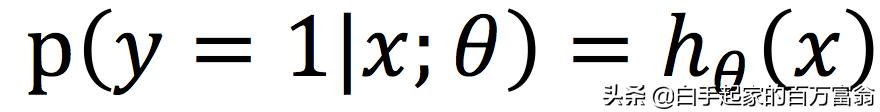
类别0的概率分别为

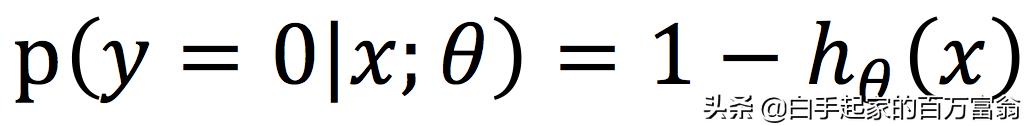
2.构造损失函数

吴恩达老师的课里面直接给出了损失函数的公式

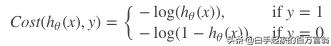
其实这个是可以通过极大似然估计来推导的，将上述概率合并为

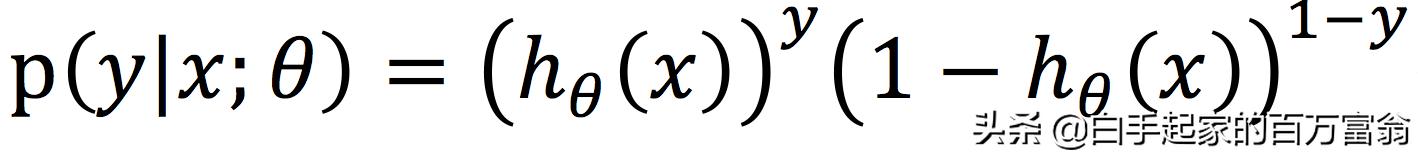
取似然函数为

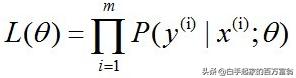
再取对数似然函数为

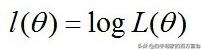
最大似然估计就是要求得使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。如果我们乘以一个负的系数-1/m，那么就可以转化为J(θ)取最小值时的θ为要求的最佳参数，这时候就用梯度下降法。

3.最小化损失函数

这里最小化损失函数的方法就是用大名鼎鼎的梯度下降法求解，式中α为学习步长，不断的迭代求偏导数，因为1/m为常量，一般也可以省略，所以最终的θ更新过程如下

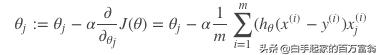
直到θ稳定后，那预测函数也就求出来了。

这就是求解逻辑回归的方法了，希望对大家有帮助，如果喜欢我的内容，请持续关注我，给我点个赞，如果有什么想法和建议请在评论区给我留言，我会继续更新~