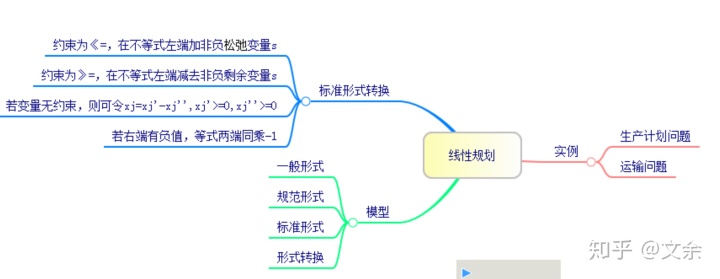
首先是线性规划模型的四种形式。要知道形式必须先知道线性规划模型是什么。
1.每个问题都用一组决策变量(x1,x2…)表示某一方案。这组决策变量的值就代表一个具体方案。一般变量非负。
2.存在一定约束条件,这些条件可用一组线性等式or线性不等式表示。
3.都有一个目标,可用决策变量的线性函数(目标函数)表示,按问题不同要求目标函数实现最大化或最小化。
满足以上条件的数学模型称为线性规划的数学模型。
定义如上,简而言之就是满足模型三要素:目标,约束,变量。
那么接下来就看看四种形式长什么样吧。



首先是线性规划模型的四种形式。要知道形式必须先知道线性规划模型是什么。
1.每个问题都用一组决策变量(x1,x2…)表示某一方案。这组决策变量的值就代表一个具体方案。一般变量非负。
2.存在一定约束条件,这些条件可用一组线性等式or线性不等式表示。
3.都有一个目标,可用决策变量的线性函数(目标函数)表示,按问题不同要求目标函数实现最大化或最小化。
满足以上条件的数学模型称为线性规划的数学模型。
定义如上,简而言之就是满足模型三要素:目标,约束,变量。
那么接下来就看看四种形式长什么样吧。


 848
848

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


