绝对值积分不等式_高数狂欢 | 积分之2017年

写在前面：

点击阅读原文获取一堆乱七八糟的高数题

2017年的积分题

                                                           by 某田

故事是这样的

某田闲来无事看了一眼公众号后台

有一个不知名小伙伴输入积分两个字

后来一想外经史也学不下去

宏观也不会

不如做一期嘻嘻

不过考虑到时间还是只做17年的了嘻嘻

如果有其他问题emmm可以后台留言哦

照惯例我们来先看选填：

第一题实际上是原函数的概念，这题千万要注意的一点是：连续函数的原函数还是连续。所以对于连续的分段函数，对几个函数分别求了不定积分以后，一定要在间断点算一下两段原函数的值，让他们保持相等，调整两个C之间的关系。

答案是D

第二题还是原函数的概念，一个是要分清楚dx啊，∫符号啊，这些符号的意义。然后用排除法就好了。

这题简单就在于B项都没有写+C...只要不是在考试的时候脑抽误以为是印刷错误的话，其实一眼就知道答案是B了...

第三题考可积的条件，

可积不一定连续，连续必定可积

有界是可积的必要条件

有界且有有限个间断点是可积的充要条件

这个题，看见A和B，就知道肯定有一个不对....

然后A和B之间选，就很好选了。无界肯定没有定积分，所以答案是A

补充，还有比如这里要知道存在比如∫1/lnxdx，∫[(e^x)/x]dx这种原函数不能用解析式表示的积分，要注意。

第四题：是一个变上限函数的问题。

这个题要求函数的极限，首先把a试着带进去，发现他是一个0/0，那么考虑洛必达。

这里一定要注意！！！变上限函数的上限不是x，是x^2，那么这里一定要对x^2求一次导。这个位置很容易忽视。

接下来就是，别忘了带进f(x)里面的应该是a^2，还好这个选项里没有干扰项。

第五题是求定积分，直接算也能算。

这个题其实用了三角函数求定积分的换元法，看一眼就能出来了。

令t=π-x，把0到2π的区间转换成-π到π的对称区间，因为sin(π-x)=sinx，加之sinx的三次方是一个奇函数，所以等于0。

奇偶函数的定积分往往能起到很大的化简作用。要格外注意。

下面演示一下普通算法怎么算...

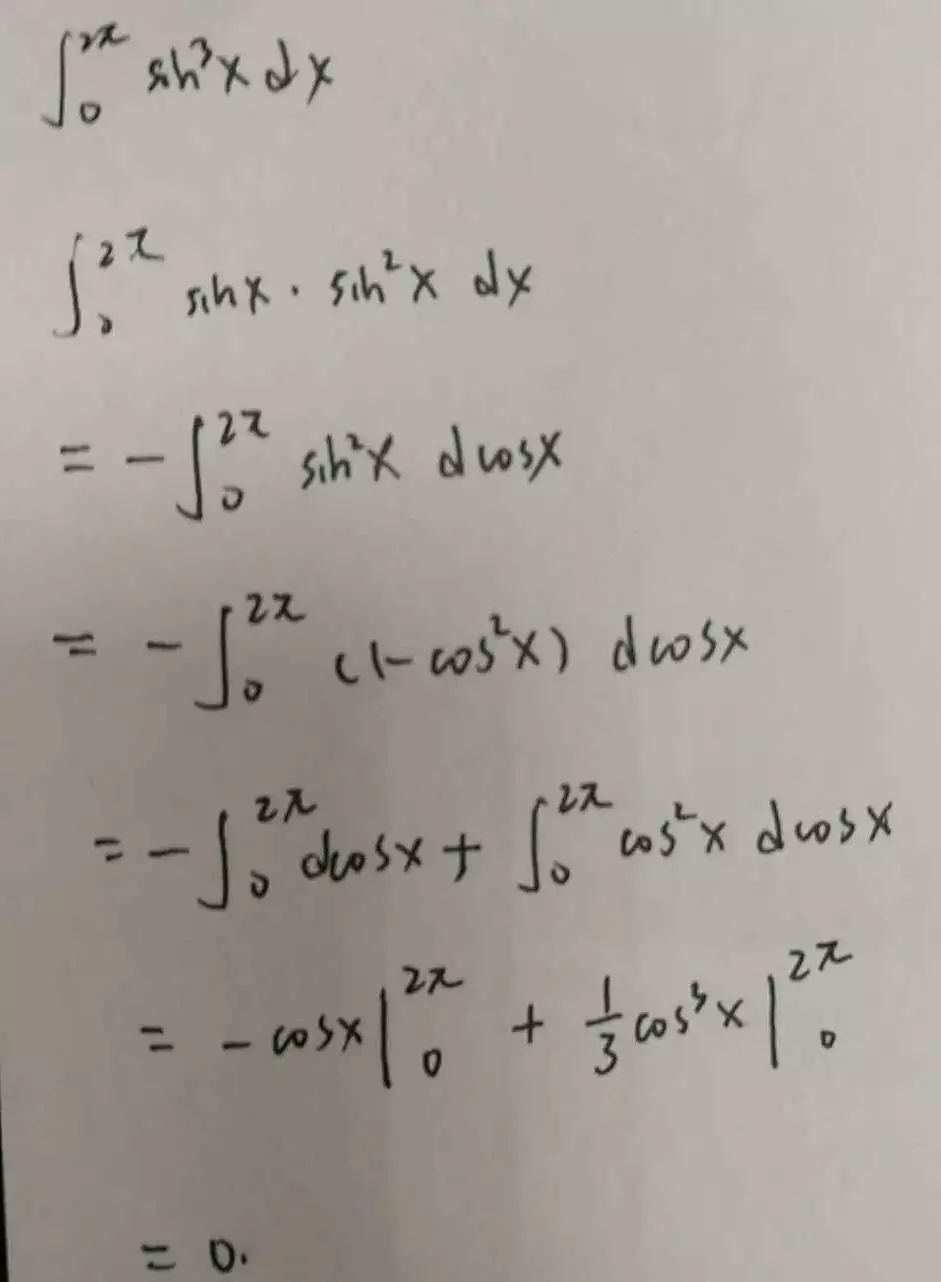
这里值得关注的是高次sinx、cosx求积分方法：

对于单独的sinx，cosx：

如果是奇数次的话，那么就单独拿出来一个sinx或cosx，变成一次和偶数次相乘的结果，对偶数次用二倍角公式慢慢降幂即可。

如果是偶数次，那就直接慢慢降幂就好....

如果有sinx的n次方和cos的相乘，或者加分式这种复杂的情况，那么：

对相乘的位置用2sinxcosx变成sin2x，或者用...万能公式，或者除以一个cosx的几次方变成tanx的函数，也有可能...

一定要小心的几个地方：一个是cosx求导会有负号，一个是sinnx和cosnx的求导会出一个n的系数。小心系数和负号上出问题。

第六题用夹角公式，把两个向量表示出来，然后算两个向量的内积(数量积)和模长，算出cosα，然后...就出来了。答案是D

第七章空间向量的题基本都不怎么难，只要能想清楚，记清公式，基本上就没问题了。

这里尤其要注意，求外积(向量积)的时候，算三阶行列式很容易出错，错的地方在于算单位k向量时，有个负号不要落下...

填空题：

第一题是不定积分，用了凑积分法，把e^x放进dx里面，把e^x看成一个整体的话，就是arctanx的导数形式了，所以答案是arctane^x，注意+C！

答案是arctane^x+C

第二题是定积分，是一个奇函数加一个偶函数，对称区间，所以前面一半是0，只要求|x|的定积分就好了。看到很复杂的定积分，先看看奇偶性，尤其是对称区间和很像对称区间的题。

答案是π^2/16

第三题是我...考试唯一错的一道题(溜了)

这道题星形线面积的填空题，要是能记住3πa^2/8的公式，这个题就...不用算了

当然这个题算起来，其实挺复杂的。

来演示一下。

当然你要大概知道星形线长啥样，是四部分完全对称的图形。

也可以带上a算一下...感觉更爽

第四题：其实是点法式平面方程的写法，很简单了，最后尽量化成平面一般方程：x+y+z-3=0

这三个计算题还不难：

第一题可以考虑换元，把分母设成t，换元后就很简单了。

第二题可以先换元，把根号x设为t，注意定积分换元必换限，然后分部积分就好了

第三题，求面积先画图，画了图之后确定积分范围！！！这里绝对不要出错，看清他要积分的是哪个区域！然后用定积分表示出来，注意上下限，然后就是算了。

这里要有一点小的知识储备，x-1和lnx在x=1点相切，知道这个就会画图了。

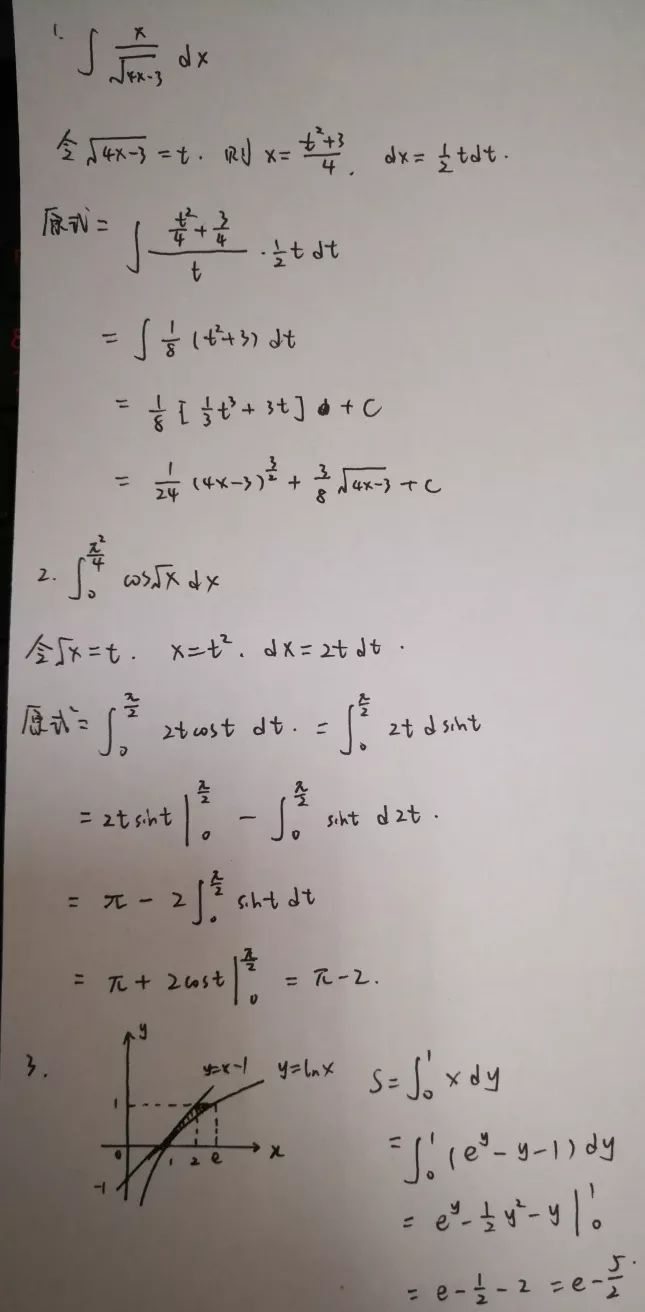
第四题...其实是我当时做的最烦的一道题...

因为我当时用分类讨论做的，分别讨论了t在不同区间范围时候的最小值，比较了之后...才算出来

感兴趣的可以试试...

这个题的正确方法要先判断出来g(0)处是极小值也是最小值。

首先我们看x是自变量，t是积分变量，这是不应该混的。

当x大于1时候，x-t一定是大于0，去掉绝对值，你会发现x越大积分值越大，所以不可能在大于1的位置。

同样，当x小于-1，去掉绝对值符号一定是t-x，x越小积分值越大，所以不可能在小于-1的位置。

接下来看x在-1到1之间，因为t也在-1到1之间，我们把绝对值去掉，记住去掉绝对值是为了算积分，不是为了算函数值，那么我们应该把积分写成：

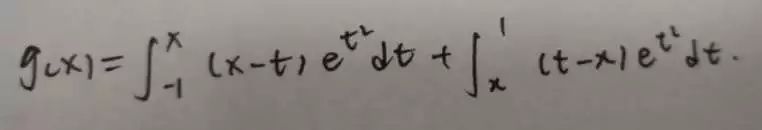
求导：

这里涉及到变上限函数更复杂的求导，因为原函数里有x，会让人蒙，但是没事！因为x不是积分变量，我们算积分的时候看成常数就好了，所以可以把x提出来，然后用乘法求导的链式法则求导：

这里是这道题最难的地方！

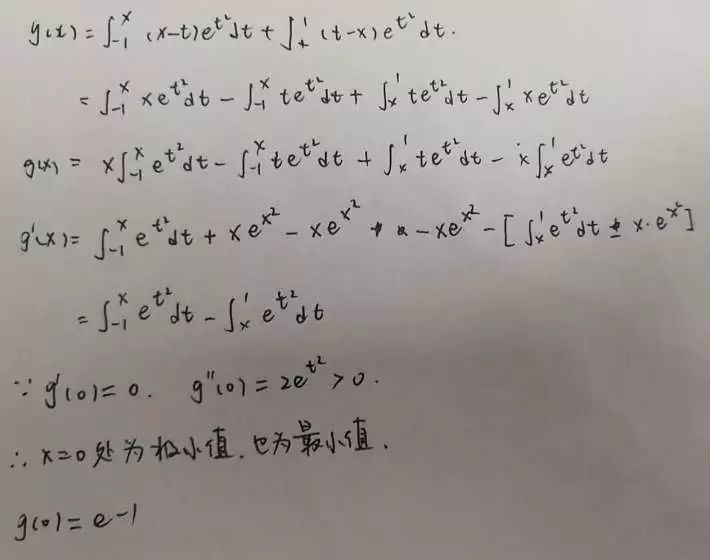
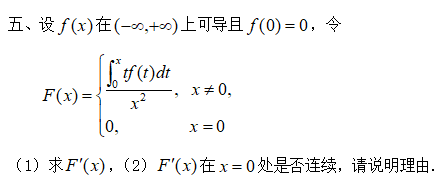
这个题...还是变上限函数...

简直有毒...

这个题第一问求导。注意在不等于0的地方直接用除法的求导式子就可以了，在等于0的位置用导数定义来求。

第二问判断连续性...只要求一下极限就可以了。

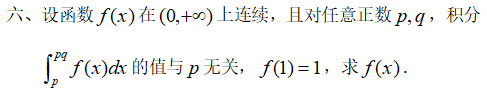
大家往往以为第六题很难。。。

其实这个题比第四题还简单...

首先要理解他让我们干什么，积分值和p无关，不管p是什么，所以p我们必须看做是一个变量。

那q呢？有人会问。q虽然也“任意”，但是题没提q变化的影响，这不是我们要研究的东西。

OK！p如果是变量...这其实又是个...变限函数...

我们看这个题的条件，怎么用数学去理解？

嘻嘻到了最后一道题

这个题看上去还挺奇怪..其实一点也不奇怪...

最关键的一步是找递推关系，这里建议大家把sinx，cosx，tanx，arctanx什么的n次方递推怎么算都看看...

一般的递推算法都需要用到分部积分。

对于这个题，这个题的递推超级好找...

看见一个递推，我们先把它的下一项写出来...

写出来你先看看直接相加减有没有什么关系，如果没有看看分部积分能不能行。基本上也就这样了...

这个题加一下直接就出来了...

好了到这里我们已经看到了曙光：

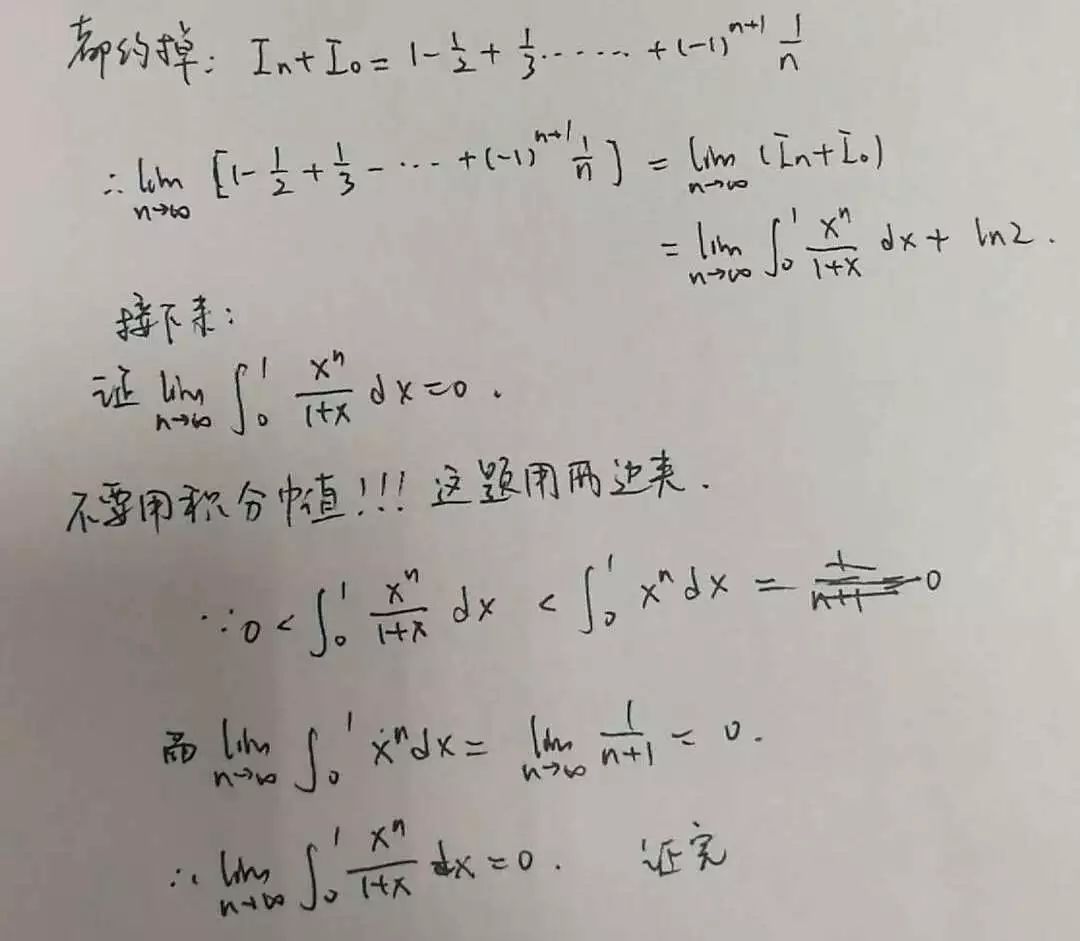
思路还是挺清晰的：

就在于一个是找到递推关系，一个是要会对递推关系进行处理。

建议大家多做做递推关系的式子。

一般来讲这种压轴题还比较喜欢出积分中值加微分中值啊，积分大小的证明啊，或者柯西施瓦茨不等式的应用这种...

随缘吧...

结论：

这套题...还行吧

积分的东西很成体系，技巧也挺多的，建议大家多练习一下，其实也还好。

祝大家考试顺利

话说我的原创类别竟然是...文学...

字好丑因为懒...

有问题可以在后台留言...

阅读原文里面试卷的提取码是disb 

...加油！

肯定没有下期了....(外经史学不完了嘤嘤嘤)

文稿 编辑 审校 | 某田

做题 | 某田

图片 | 某田