tensorflow打印模型结构_TensorFlow Probability概率编程时序模型

最新推荐文章于 2024-01-07 05:00:00 发布

weixin_39757893

最新推荐文章于 2024-01-07 05:00:00 发布

阅读量420

点赞数

文章标签： tensorflow打印模型结构

简介：本文使用TensorFlow Probability这一新的概率编程工具，通过实例介绍其中的时间序列建模。

一、背景

2018年在加利福尼亚州山景城召开的TensorFlow开发者峰会上，Google宣布了新的工具----TensorFlow Probability。TensorFlow Probability是一种提供先进贝叶斯建模的概率编程工具，作为Google当下力推的人工智能框架，当然也享有TensorFlow的便利--跨平台、多语言支持，以及针对机器学习和深度学习对算力要求颇高的分布式并行与GPUs/TPUs计算资源。更早的2017年Google便开发了深度概率编程语言Edward，加之最新更新的TensorFlow2.0，TensorFlow俨然构成了一个巍巍壮观的机器学习生态群。

本文作者刚好在处理时间序列方面的应用，尝试了TensorFlow Probability，相对而言大家对于频率学派的统计机器学习更熟悉，加之TensorFlow Probability开源刚一年，鉴于当下相关资料非常少，尤其是时间序列模块是后来加入到TensorFlow Probability中，本文作为一种应用和介绍性质的推送，不会涉及过多公式等细节，更多的用贝叶斯建模在TensorFlow Probability上实现时间序列建模，探索其效果。机器学习的特点正是模型花样繁多，通常针对具体领域和不同的数据集尝试找到最优表现的模型，正如George E. P. Box那句振聋发聩的名言：“All models are wrong, but some are useful”。

关键词：TensorFlow Probability ；概率编程；贝叶斯；时间序列

二、概率编程与TensorFlow Probability介绍

贝叶斯建模的特点是引入先验信息，通过概率描述不确定；概率编程则是利用计算机采样的方法进行贝叶斯推断(Bayesian inference)，得出未知参数的概率分布，也就是利用贝叶斯公式给定观测数据和先验分布计算参数的后验概率，公式如下：

由于后验分布精确求解非常困难，所以使用变分推断(variational inference)作为近似解来代替，将计算后验分布转化为优化问题，常用的优化/损失函数为ELBO(negative evidence lower bound)，通过循环迭代直至收敛，得到变分参数。

以上是基本概念介绍，下面我们先从整体上看看TensorFlow Probability都有哪些主要内容。

图 1(来源于tensorflow官网)

如上图可见，主要包含：分布、模型构建层/损失函数、马尔可夫概率推断、优化。通过 Bijectors 和 TransformedDistribution计算复杂的分布，使用tfp.mcmc，tfp.vi进行概率推断。

本文主要针对贝叶斯结构时间序列/Structural time series (STS)这个模块，类似于R的BSTS包，为便于复现(tensorflow安装过程中可能会存在一些小问题，版本升级快，不同版本之间差异大),先声明运行环境：

CentOS Linux 7.4；
tensorflow ==1.13.1 ;
tensorflow-probability==0.6.0

建模部分正是上文提到的概率编程的过程，本文主要分为以下步骤：

将训练数据输入-输出映射；
使用变分推断拟合模型，抽样计算参数后验分布；
得到模型预测值；
计算模型评估指标MAPE；

三、Python编程实现

#导入模型import numpy as npimport pandas as pdimport tensorflow as tfimport tensorflow_probability as tfpfrom tensorflow_probability import distributions as tfdfrom tensorflow_probability import stsimport warningswarnings.filterwarnings("ignore")#读取数据data_t=pd.read_csv("../input/example_ts.csv")#过滤TF输出信息export TF_CPP_MIN_LOG_LEVEL=3

下面看看数据折线图,反映了销量在时间上的变化，由图2可见该序列是有局部线性趋势且呈现一定的季节性，以年为周期。

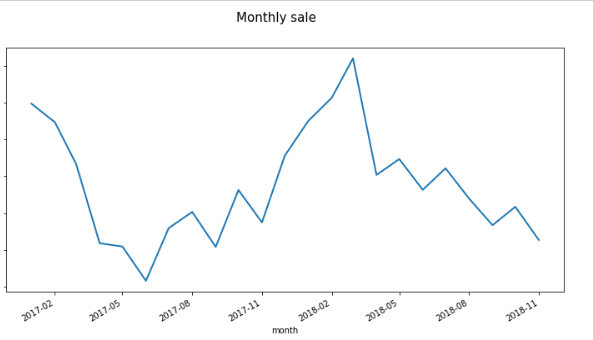
图 2

程序运算步骤主要为：用正态分布作为先验分布，使用negative evidence lower bound (ELBO)作为损失函数，通过tfp.sts 计算后验。

主要代码如下：

#建构模型，并计算计算损失函数def cal_loss(training_data):        #设置全局默认图形    tf.reset_default_graph()    #遵循加法模型，设置趋势    trend = sts.LocalLinearTrend(observed_time_series=observed_time_series)        #设置季节性    seasonal = tfp.sts.Seasonal(          num_seasons=12, observed_time_series=observed_time_series)    #模型拟合,之所以用sum，而不是我们在建模中常见的fit定义，是因为，    #模型时间序列为加法模型，有如上文提到的趋势，季节性，周期性等成分相加    #默认的先验分布为正态(normal)    ts_model = sts.Sum([trend, seasonal], observed_time_series=observed_time_series)    #构建变分损失函数和后验    with tf.variable_scope('sts_elbo', reuse=tf.AUTO_REUSE):        elbo_loss, variational_posteriors = tfp.sts.build_factored_variational_loss(          ts_model,observed_time_series=training_data)        return ts_model,elbo_loss,variational_posteriors#模型训练，输出后验分布def run(training_data):        ts_model,elbo_loss,variational_posteriors=cal_loss(training_data)    num_variational_steps = 401     num_variational_steps = int(num_variational_steps)    #训练模型，ELBO作为在变分推断的损失函数    train_vi = tf.train.AdamOptimizer(0.1).minimize(elbo_loss)        #创建会话,并通过上下文管理器方式对张量Tensor对象进行计算    with tf.Session() as sess:        sess.run(tf.global_variables_initializer())        for i in range(num_variational_steps):            _, elbo_ = sess.run((train_vi, elbo_loss))                    if i % 20 == 0:            print("step {} -ELBO {}".format(i, elbo_))        #求解后验参数        q_samples_ = sess.run({k: q.sample(3)                             for k, q in variational_posteriors.items()})                        print("打印变分推断参数信息:")        for param in ts_model.parameters:            print("{}: {} +- {}".format(param.name,                      np.mean(q_samples_[param.name], axis=0),                      np.std(q_samples_[param.name], axis=0)))    data_t_dist = tfp.sts.forecast(ts_model,observed_time_series=training_data,\                                   parameter_samples=q_samples_,num_steps_forecast=num_forecast_steps)    return  data_t_dist#模型预测def forecast(training_data):    data_t_dist=run(training_data)    with tf.Session() as sess:        data_t_mean, data_t_scale, data_t_samples = sess.run(          (data_t_dist.mean()[..., 0],           data_t_dist.stddev()[..., 0],           data_t_dist.sample(num_samples)[..., 0]))            return data_t_mean,data_t_scale, data_t_samples#计算回测def get_mape(data_t,forecsat):    true_=data_t[-num_forecast_steps:]    true_=true_.iloc[:,-1]    true_=true_.reset_index()    forecsat=pd.DataFrame(forecsat,columns=['focecast'])    mape_=pd.concat([pd.DataFrame(true_),forecsat],axis=1)    mape_['mape']=abs(mape_.iloc[:,-2]-mape_.iloc[:,-1])/mape_.iloc[:,-2]*100    return mape_

(更精彩的代码内容请向右滑动)

完成了时间序列建模还不够，我们需要对模型效果和结果进行评估，一个完整的时间序列模型效果评估，应包含以下三部分：

模型整体拟合指标
模型效果评估指标
模型系数指标

下面分别给与解释，ELBO作为模型相对评估指标，作为模型选择指标，在构建多个模型的时，选择ELBO最小的那个模型，只是表明完成了模型的拟合程度，并不能作为单一模型好坏的评估依据。正如回归模型的RMSE，拟合完成后还需要对模型整体是否有意义进行解读，在回归模型中我们一般使用R方来判断模型好坏，时间序列常用的指标为MAPE，MAPE越小越好。本次输出的模型系数指标有：

observation_noise_scale
LocalLinearTrend/level_scale
LocalLinearTrend/slope_scale
Seasonal/_drift_scale；
分别表示，噪声，局部线性截距，局部线性趋势的斜率，季节性四个系数，从本例得出的置信区间来看，以上指标皆显著。为便于理解，做个类比，一般来说一个最简单的(未标准化/归一化)线性回归也应该包含三个因素：

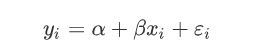
即，截距(intercept )，回归(slope of the regression)，残差(residual)，亦如时序加法模型的局部线性，季节性等因素。

下图为模型输出结果图，其中橘黄色为100次抽样的结果，红色为后验分布得出参数----期望，即，我们要预测的值，从图3中我们可以看出，预测值与真实值(销量)很接近，我们用时间序列的回测(Backtesting)MAPE作为模型评估指标，本次在该程序实例上MAPE为9%，表现非常不错，为进一步测试模型的效果，作者选择了个399时间跨度超过15个月的sku序列，最终模型得到的回测结果为16%，由此可见TensorFlow Probability提供的时间序列建模模块一个值得尝试的工具。

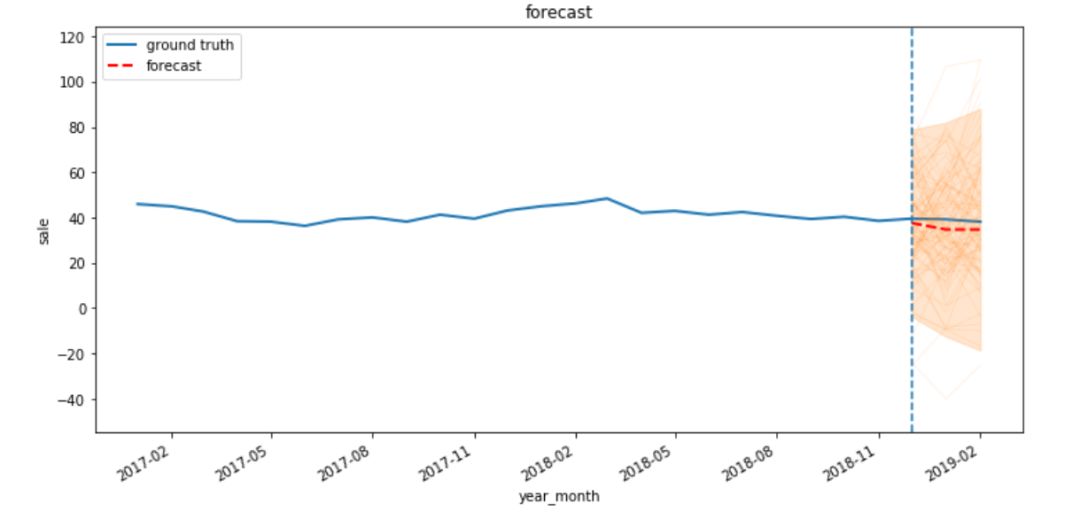
图 3

除了上文讲到的使用贝叶斯概率编程建模，还有另一个模型训练技巧也被我们常用到，那就是贝叶斯优化(Bayesian Optimization)，我们知道在模型训练过程中为了得到最优模型表现，以最小的损失函数值为目标，常常使用网格搜索寻找最优参数，但这非常耗时间，当模型的超参数很多时，大大增加了计算量，尤其是在神经网络这种复杂度非常高的模型中，针对某一个参数进行循环都需要花费不少力气，为了降低搜索空间，提高运算效率同时在兼顾模型效果的时候，我们会用到贝叶斯优化来寻找最优参数。

四、展望

本文对这一工具做了简单介绍并通过一个实例，呈现了TensorFlow Probability概率编程在时序模型上的使用，还有非常多可以扩展的地方，如果依然聚焦在时间序列模型方面，那么有以下几点可以进一步完善：

部署大规模时序模型；
使用贝叶斯优化调节超参数;
使用多元时序预测。

如本文开头所说，TensorFlow Probability可以使用TensorFlow 的GPUs和并行分布式部署，针对贝叶斯运算需要较大的算力和拥有大规模的时间序列模型训练，且需要在短时间内(如程序需在3个小时之内)完成，TensorFlow Probability优势就比较明显了。官方使用的例子中还使用了更复杂的多元时间序列，想进一步深入，或者真正从应用角度开始，请参阅官方文档，同时官方简介给出了入门参考书。

图 4

好消息是这本书有中文版，实用性较强，没有过多的公式，也因此该书讲解的较浅，可以作为入门如果要收其全功，知其所以然，还需要花费较大的力气去从原理公式着手。

五、总结

即使贝叶斯概率模型作为一种新的建模范式，依然遵循经典的时序模型建模原理，如时序的季节性，增长趋势因素的可加性(加法模型)。TensorFlow Probability作为一种先进的工具，在市面上介绍贝叶斯时序建模资料不多的情况下，本文从工具本身、基本概率、建模步骤等方面做了简单介绍，最后通过模型的评估指标(MAPE)来看，模型表现效果良好。由于贝叶斯概率建模有较高的准入门槛且还依赖于对TensorFlow提前熟悉，本工具即使有Google强力背书且开发团队不乏名校硕博，但毕竟是一个新出生的工具，尚且没有经过多少迭代，不少功能和细节没有完善，如果从企业级应用来讲，以此来大规模部署需要小心。本文作为工具开箱使用简介，作为对时间序列建模的一种新尝试，写就此文，并以此共勉；如有误，欢迎交流并指出。

参考资料

https://www.jiqizhixin.com/articles/042202
https://github.com/tensorflow/probability
Pattern Recognition and Machine Learning

欢迎关注本公众号