历届试题 区间k大数查询（优化算法）

问题描述

给定一个序列，每次询问序列中第l个数到第r个数中第K大的数是哪个。

输入格式

第一行包含一个数n，表示序列长度。

第二行包含n个正整数，表示给定的序列。

第三个包含一个正整数m，表示询问个数。

接下来m行，每行三个数l,r,K，表示询问序列从左往右第l个数到第r个数中，从大往小第K大的数是哪个。序列元素从1开始标号。

输出格式

总共输出m行，每行一个数，表示询问的答案。

样例输入

5
1 2 3 4 5
2
1 5 2
2 3 2

样例输出

4
2

数据规模与约定

对于30%的数据，n,m<=100；

对于100%的数据，n,m<=1000；

保证k<=(r-l+1)，序列中的数<=106。

 

解题思路：

此题有一种暴力解决方法是每定一个区间的第X大时，就把区间内的值取出排序，取第X大的数，但很明显，当n，m足够大，暴力就显得很浪费时间。

所以采取一开始对n个数进行排序，排序时输入顺序也要对应记录下。然后以下面的例子说明，倘若输入9个数：

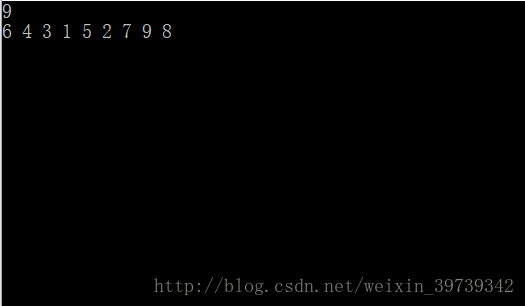
然后进行一次排序

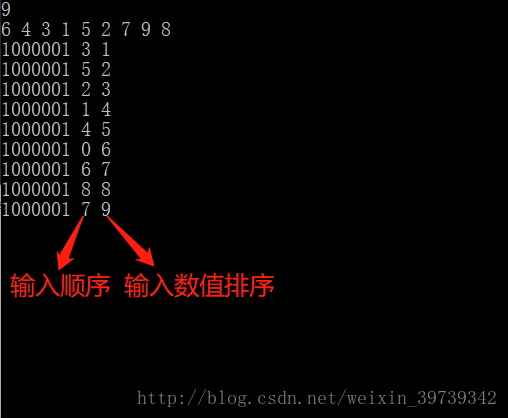
随后我们输入区间和取得第X大，假如是第2个输入到第8个输入（即是上图输入顺序的1到7），第4大的话，我们可以从上图的输入顺序，由下往上进行判断是否满足输入区间，是则计一，不是则过，计到等于X时，对应的值即为第X大。

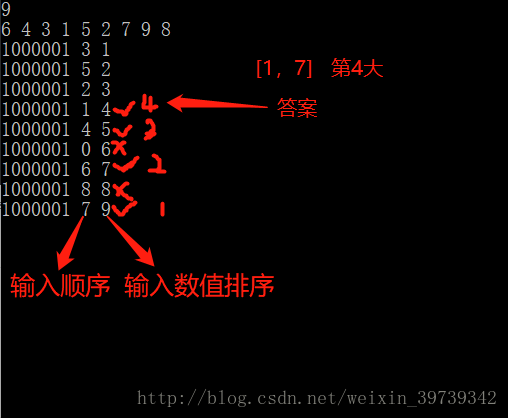
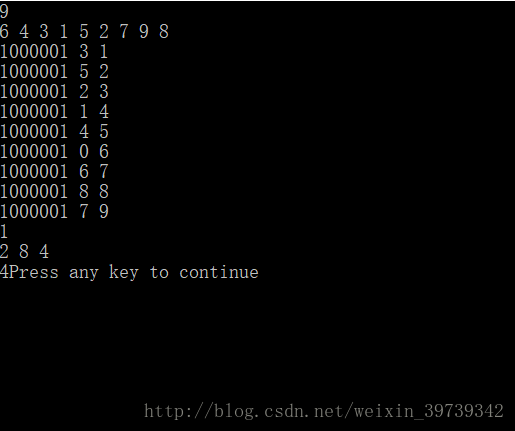
以此方法可适应大量数据，只需要做一次排序，不需要重复排序，对于大量数据，时间复杂度会明显降低。

#include"stdio.h"
long def(long i[2][1000],int l,int r,int num,int K);

int main()
{
	int num,n,m,min,Min,X=0;
	long i[3][1000];
	scanf("%d",&num);
	for(n=0;n<num;n++)
	{
		scanf("%ld",&i[0][n]);
	}
	i[0][n]=NULL;
	for(n=0;n<num;n++)
		i[1][n]=-1;

	while(1)
	{
		for(n=0;n<num;n++)
		{
			if(i[0][n]<1000000){min=i[0][n];Min=n;break;}
		}
		if(Min==-1)break;
		for(n++;n<num;n++)
		{
			if(i[0][n]<min){min=i[0][n];Min=n;}
		}
		i[0][Min]=1000001;
		i[1][X]=Min;
		i[2][X++]=min;
		Min=-1;
	}
	//for(n=0;n<num;n++)
		//printf("%ld %ld %ld\n",i[0][n],i[1][n],i[2][n]);

    scanf("%d",&m);
	int l,r,K;
	long key[1000];
	for(n=0;n<m;n++)
	{
		scanf("%d %d %d",&l,&r,&K);
		key[n]=def(i,l-1,r-1,num,K);
	
	}
	key[n]=NULL;
	for(r=0;r<n;r++)
	{
		printf("%ld",key[r]);
		if(r+1!=n)printf("\n");
	}
 
    return 0;
}

long def(long i[3][1000],int l,int r,int num,int K)//输出第K大的数值
{
	int n,key=0;
	long a;
	for(n=num-1;n>=0;n--)
	{
		if(i[1][n]>=l&&i[1][n]<=r)key++;
		if(key==K)return i[2][n];
	}
	return 1;

}