堆排序时间复杂度_py排序-堆排序heapSort

最新推荐文章于 2024-08-16 08:47:08 发布

最新推荐文章于 2024-08-16 08:47:08 发布 · 254 阅读

文章标签：

#堆排序时间复杂度

本文详细介绍了堆排序算法的原理与步骤，包括如何构建初始堆、调整堆结构以保持堆特性，以及如何通过反复交换和重建堆来实现序列排序。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

堆排序思想：

堆排序，利用堆这种数据结构设计的一种排序算法，是选择排序的一种。
堆是一种近似完全二叉树的数据结构，并且：子节点的键值或索引总是小于（或者大于）它的父节点。

算法描述：

构造初始堆。将给定无序序列构造成一个堆（一般升序采用大顶堆，降序采用小顶堆)；
将堆顶元素与末尾元素进行交换，使末尾元素最大/最小，则末尾就是排好序的数组。
然后继续调整堆为大顶堆/小顶堆。
再将堆顶元素与末尾元素交换，得到第二大元素；
重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素；
如此反复进行交换、重建、交换，直到整个序列有序。

参考：

https://zhuanlan.zhihu.com/p/73714165
https://zhuanlan.zhihu.com/p/142673431
南风以南：python实现·十大排序算法之堆排序(Heap Sort)

我的理解之大白话：

好不容易看懂了，咱必须得唠唠，（害，写的啥玩意，感觉语句不通的）：

首先，堆，大顶堆，小顶堆的定义都很明显。下图里左右分别为大顶堆和小顶堆。

https://blog.youkuaiyun.com/qq_28063811/article/details/93034625

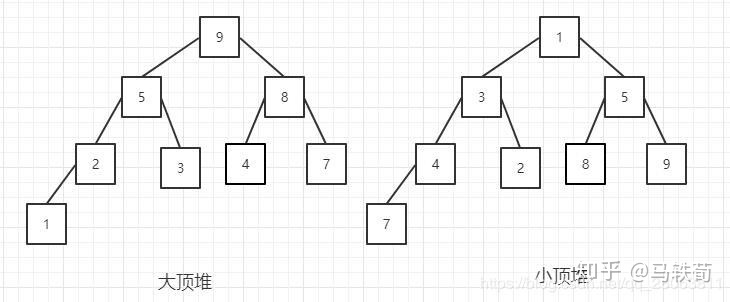
2. 我在思考的时候，就觉得有三个问题骚扰着我：

列表和树怎么建立关系？
- emmm很简单，例如上面那个大顶堆，写成数组就是[9,5,8,2,3,4,7,1]
- 哈哈哈其实就是树的按行读取啦。
- 所以不要怀疑，[9,5,8,2,3,4,7,1]就是上面那棵树，上面那棵树就是[9,5,8,2,3,4,7,1]
- 对于待排序序列：[91, 60, 96, 13, 35, 65, 46, 65, 10, 30, 20, 31, 77, 81,22]，我们先给他画成树的形式。如下图，而我们的目标是把他转化为大顶堆。

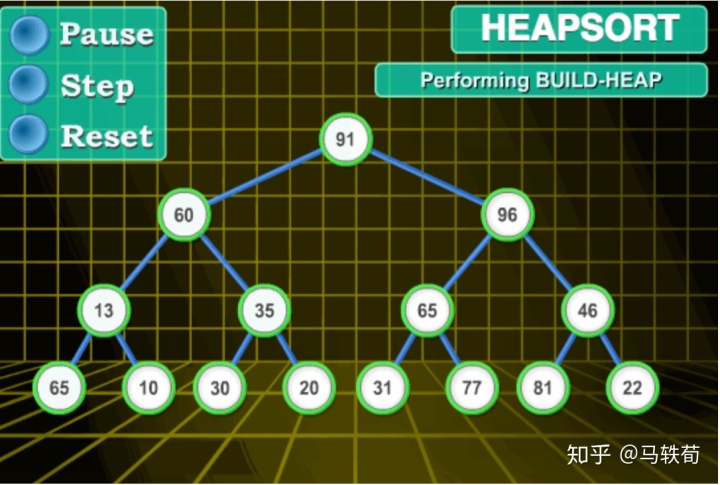
我怎么把给序列的一般树排序成大顶堆呢？
- 这就是堆排序算法里的重点了，我们将问题拆解，根据堆关于父子节点数值问题的定义，其实这个树可以拆解为众多的父节点和子节点组，比如上图，基本单位就是[91,60,96] [60,13,35] [96,65,46], [13,65,10], [35,30,20], [65,31,77], [46,81,22]。我们只要保证这些基本单位都满足堆的定义，那么就肯定没得问题了。
- 那么问题来了，怎么确保单元内部满足堆的条件呢？
  - 首先需要解决的就是，数组id和数据在树中的位置关系。在数组里，父节点和字节点怎么确定，那么通过找规律我们可以发现，父节点index是 n 的话，那么其左右节点就是 2n+1 , 2n+2。
  - 那么基本单位的排序顺序怎么订？我们是从上而下调整基本单位？还是从下而上呢？答案是从下而上。有人回答啦，我觉得还挺在理：“堆是一个二叉树，以最大堆为例，建堆的本质是让这颗二叉树满足父节点的值大于等于子节点节点。自底向上本质上就是一个倒序的层次遍历，每个层上的元素与自己的孩子比较一下，保证自己大于子节点，最后堆顶一定是最大值。通过层层向上的方式，符合堆性质的区域从底层向上扩张，最终建堆完成。如果是自顶向下，当第i层和他的孩子i+1层比较中出现交换，交换后的i层不能保证小于i-1层，于是又要向上验证，最坏情况是验证到顶。”
    链接在这：https://www.zhihu.com/question/65501536
  - 然后既然是基本单元，就知道肯定存在迭代的啦。出现交换的话肯定要迭代进行判断交换后的是否依旧满足。这个代码中会体现。
排成这个样子之后我怎么取出来？
- 问题来了，我排成大顶堆，只能说最顶层的数值最大，其他还是不确定，也不能得到排序后的结果。
- 这就对了，我们排好大顶堆之后啊，其实只能拿到一个最大的值，咱们就默默的把他和数组最后一位的数据进行交换，那么咱们的最后一位数字是不是就相当于排序好了呀。然后刚才本来的最后一位被放在根节点了，这又不是大顶堆了，我们就需要对这个交换后的树重新堆排序，再排个第二大的数据出来，当然这个去排序的树，肯定要砍掉刚才被放到最后一位的最大数了。
- 然后就是拿出一位最大数，再堆排序，再拿，直到全部排完，我们就结束啦。

写了半天，咱也不知道自己写了个啥玩意。上代码吧还是您。

python代码实现：

def buildHeap(sortList,lenS,target):
    # 堆树的基本单元进行整理
    largest = target
    left,right = 2*target+1, 2*target+2
    # 如果是逆序排序，直接把下面两个if里面的大于号换成小于号，构建小顶堆就行了
    if left<lenS and sortList[left]>sortList[target]: largest = left
    if right<lenS and sortList[right]>sortList[largest]: largest = right
    if largest != target:
        sortList[largest],sortList[target] = sortList[target],sortList[largest]
        # 发生交换，则进行迭代整理
        buildHeap(sortList,lenS,largest)

def heapSort(sortList):
    lenS = len(sortList)
    # 最后一个父节点的id
    last_root = lenS//2-1
    # 自底向上构建堆
    for i in range(last_root,-1,-1):
        buildHeap(sortList, lenS, i)
    # 取出堆顶元素，进行排序
    for end in range(lenS-1, 0, -1):
        sortList[0], sortList[end] = sortList[end], sortList[0]
        # end每次都会减1，所以就自动排除后面已经排序好的数据了
        buildHeap(sortList, end, 0)
    return sortList

print(heapSort([1,9,8,6,9,2,9,5,4,3,8]))