题目所在试卷参考答案:
数学答案
一、 选择题(本题共12个小题,每小题3分,满分36分)题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D B D C B C C C A C C
二、填空题(本大题共6个小题,每小题3分,满分18分)
13. 2 ;14. ;15. y=﹣
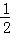 x+
x+
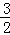 ;16.a≤-1 ; 17.x=3或x≥6; 18. (20,0)
;16.a≤-1 ; 17.x=3或x≥6; 18. (20,0)
三、解答题(本大题共7小题,满分66分)
19.(本题满分6分)
原式= ..........3分
原式=1 ..........6分
20. (本题满分8分) 解:(1)a=5÷12.5%×40%=16,5÷12.5%=7÷b%,
∴b=17.5,
故答案为:16,17.5;..............2分
(2)600×[6÷(5÷12.5%)]=90(人),
故答案为:90;.................4分
(3)如图,∵共有20种等可能的结果,两名主持人恰为一男一女的有12种情况,
∴则P(恰好选到一男一女)=
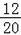 =
=
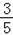 .
.
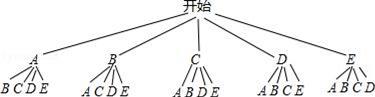
.........8分
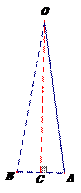
21. (本题满分9分)(1) 图1,作OC⊥AB,
∵OA=OB, OC⊥AB,∴AC=BC, ∠AOC=∠BOC=∠AOB=9°,
在Rt△AOC 中,sin∠AOC = , ∴AC≈0.1564×10=1.564,
∴AB=2AC=3.128≈3.13.
∴所作圆的半径是3.13cm. ............4分
 (2)图2,以点A为圆心,AB长为半径画弧,交OB于点C, 作AD⊥BC于点D;
(2)图2,以点A为圆心,AB长为半径画弧,交OB于点C, 作AD⊥BC于点D;
∵AC=AB, AD⊥BC,
∴BD=CD, ∠BAD=∠CAD=∠BAC,
∵∠AOB=18°,OA=OB ,AB=AC,
∴∠BAC=18°, ∴∠BAD=9°,
在Rt△BAD 中, sin∠BAD = ,
∴BD≈0.1564×3.128≈0.4892,
∴BC=2BD=0.9784≈0.98
∴铅笔芯折断部分的长度约为0.98cm. ..............9分
22. (本题满分9分)
解:(1)由题意知,若观光车能全部租出,则0<x≤100,
由50x﹣1100>0,
解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元;................3分
(2)设每天的净收入为y元,
当0<x≤100时,y1=50x﹣1100,
∵y1随x的增大而增大,
∴当x=100时,y1的最大值为50×100﹣1100=3900;
当x>100时,
y2=(50﹣
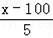 )x﹣1100
)x﹣1100
=﹣
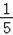 x2+70x﹣1100
x2+70x﹣1100
=﹣
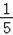 (x﹣175)2+5025,
(x﹣175)2+5025,
当x=175时,y2的最大值为5025,
5025>3900,
故当每辆车的日租金为175元时,每天的净收入最多是5025元........9分
23. (本题满分11分)
(1)证明:连接AD,
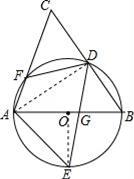 ∵AB是⊙O的直径,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;............3分
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°﹣∠E,
又∵∠CFD=180°﹣∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;...........5分
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB=
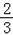 ,BD=4,
,BD=4,
∴AB=6,
∵E是
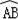 的中点,AB是⊙O的直径,
的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3
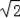 ,
,
∵E是
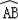 的中点,
的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴
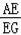 =
=
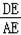 ,
,
即EG•ED=AE2=18................11分
24. (本题满分9分)
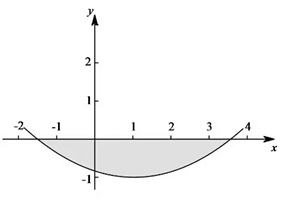
解析:(1)将抛物线表达式变为顶点式
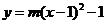 ,则抛物线顶点坐标为(1,-1);.............2分
,则抛物线顶点坐标为(1,-1);.............2分
(2)①m=1时,抛物线表达式为
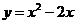 ,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;..4分
,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;..4分
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;又有抛物线表达式,令y=0,则
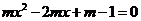 ,得到A、B两点坐标分别为(
,得到A、B两点坐标分别为(
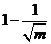 ,0),(
,0),(
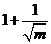 ,0),即5个整点是以(1,0)为中心向两侧分散,进而得到
,0),即5个整点是以(1,0)为中心向两侧分散,进而得到
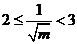 ,∴
,∴
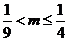 ..............9分
..............9分
25. (本题满分14分)
解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,
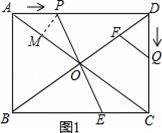 ∴AC=10,
∴AC=10,
①当AP=PO=t,如图1,过P作PM⊥AO,
∴AM=
 AO=
AO=
 ,
,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ADC,
∴
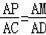 ,
,
∴AP=t=
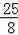 ,
,
②当AP=AO=t=5,
∴当t为
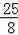 或5时,△AOP是等腰三角形;...........3分
或5时,△AOP是等腰三角形;...........3分
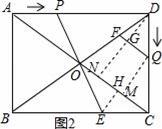
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,
在△APO与△CEO中,
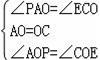 ,
,
∴△AOP≌△COE,
∴CE=AP=t,
 ∵△CEH∽△ABC,
∵△CEH∽△ABC,
∴
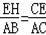 ,
,
∴EH=
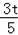 ,
,
∵DN=
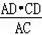 =
=
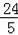 ,
,
∵QM∥DN,
∴△CQM∽△CDN,
∴
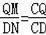 ,即
,即
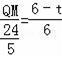 ,
,
∴QM=
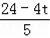 ,
,
∴DG=
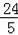 ﹣
﹣
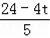 =
=
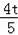 ,
,
∵FQ∥AC,
∴△DFQ∽△DOC,
∴
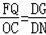 ,
,
∴FQ=
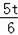 ,
,
∴S五边形OECQF=S△OEC+S四边形OCQF=
 ×5×
×5×
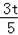 +
+
 (
(
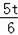 +5)•
+5)•
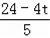 =﹣
=﹣
 t2+
t2+
 t+12,
t+12,
∴S与t的函数关系式为S=﹣
 t2+
t2+
 t+12;...........8分
t+12;...........8分
(3)存在,
∵S△ACD=
 ×6×8=24,
×6×8=24,
∴S五边形OECQF:S△ACD=(﹣
 t2+
t2+
 t+12):24=9:16,
t+12):24=9:16,
解得t=
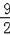 ,t=0,(不合题意,舍去),
,t=0,(不合题意,舍去),
∴t=
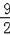 时, S五边形OECQF:S△ACD=9:16;
时, S五边形OECQF:S△ACD=9:16;
(4)如图3,过D作DM⊥PE于M,DN⊥AC于N,
∵∠POD=∠COD,
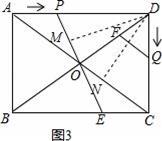 ∴DM=DN=
∴DM=DN=
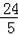 ,
,
∴ON=OM=
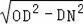 =
=
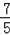 ,
,
∵OP•DM=3PD,
∴OP=5﹣
 t,
t,
∴PM=
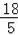 ﹣
﹣
 t,
t,
∵PD2=PM2+DM2,
∴(8﹣t)2=(
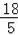 ﹣
﹣
 t)2+(
t)2+(
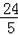 )2,
)2,
解得:t=16(不合题意,舍去),t= ,
∴当t= 时,OD平分∠COP.................14分







 本文详细解答了数学竞赛中的选择题、填空题和解答题,涉及范围包括几何、代数、概率等多个数学知识点,提供了精准的计算步骤和解题思路。关键部分包括圆周率计算、等比数列、函数解析、三角函数应用、几何图形的计算、线性方程组、不等式求解、概率分布、圆的半径确定等。
本文详细解答了数学竞赛中的选择题、填空题和解答题,涉及范围包括几何、代数、概率等多个数学知识点,提供了精准的计算步骤和解题思路。关键部分包括圆周率计算、等比数列、函数解析、三角函数应用、几何图形的计算、线性方程组、不等式求解、概率分布、圆的半径确定等。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








