判断深度学习模型的稳定性_人工智能干货｜一线工程师带你学习深度学习模型量化理论+实践...

2019年的最后一天，送给自己一份特殊的礼物。

模型量化作为一种能够有效减少模型大小，加速深度学习推理的优化技术，已经得到了学术界和工业界的广泛研究和应用。模型量化有 8/4/2/1 bit等，本文主要讨论目前相对比较成熟的 8-bit 低精度推理。 通过这篇文章你可以学习到以下内容：1)量化算法介绍及其特点分析，让你知其然并知其所以然； 2)Pytorch 量化实战，让你不再纸上谈兵；3)模型精度及性能的调优经验分享，让你面对问题不再束手无策；4)完整的量化文献干货合集，让你全面系统地了解这门主流技术。

1.CPU 推理性能提升 2-4 倍，模型大小降低至1/4，模型量化真的这么好使？

维基百科中关于量化(quantization)的定义是: 量化是将数值 x 映射到 y 的过程，其中 x 的定义域是一个大集合(通常是连续的)，而 y 的定义域是一个小集合(通常是可数的)【1】。8-bit 低精度推理中， 我们将一个原本 FP32 的 weight/activation 浮点数张量转化成一个 int8/uint8 张量来处理。模型量化会带来如下两方面的好处：

• 减少内存带宽和存储空间

深度学习模型主要是记录每个 layer(比如卷积层/全连接层) 的 weights 和 bias, FP32 模型中，每个 weight 数值原本需要 32-bit 的存储空间，量化之后只需要 8-bit 即可。因此，模型的大小将直接降为将近 1/4。

不仅模型大小明显降低， activation 采用 8-bit 之后也将明显减少对内存的使用，这也意味着低精度推理过程将明显减少内存的访问带宽需求，提高高速缓存命中率，尤其对于像 batch-norm， relu，elmentwise-sum 这种内存约束(memory bound)的 element-wise 算子来说，效果更为明显。

• 提高系统吞吐量(throughput)，降低系统延时(latency)

直观理解，试想对于一个 专用寄存器宽度为 512 位的 SIMD 指令，当数据类型为 FP32 而言一条指令能一次处理 16 个数值，但是当我们采用 8-bit 表示数据时，一条指令一次可以处理 64 个数值。因此，在这种情况下，可以让芯片的理论计算峰值增加 4 倍。在CPU上，英特尔至强可扩展处理器的 AVX-512 和 VNNI 高级矢量指令支持低精度和高精度的累加操作，详情可以参考文献【2】。

2.量化设计

按照量化阶段的不同，一般将量化分为 quantization aware training(QAT) 和 post-training quantization(PTQ)。QAT 需要在训练阶段就对量化误差进行建模，这种方法一般能够获得较低的精度损失。PTQ 直接对普通训练后的模型进行量化，过程简单，不需要在训练阶段考虑量化问题，因此，在实际的生产环境中对部署人员的要求也较低，但是在精度上一般要稍微逊色于 QAT。本文介绍的主要方法也是针对 PTQ 。关于 QAT 的内容，因为理论较为复杂，我打算后续重新写一篇文章详细介绍。

在介绍量化算法之前，我们先看一下浮点数和 8-bit 整数的完整表示范围。

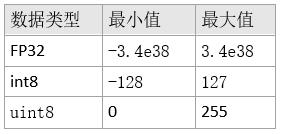
表1 数据表示范围

量化算法负责将 FP32 数据映射到 int8/uint8 数据。实际的 weight/activiation 浮点数动态范围可能远远小于 FP32 的完整表示范围，为了简单起见，在下面的量化算法介绍中，我们直接选取 FP32 张量的最大值(max)和最小值(min)来说明量化算法，更为详细的实际动态范围确定方法将在后续部分说明。量化算法分为对称算法和非对称算法，下面我们主要介绍这两种算法的详细内容及其区别。

• 非对称算法 (asymmetric)

如下图所示，非对称算法那的基本思想是通过 收缩因子(scale) 和 零点(zero point) 将 FP32 张量 的 min/max 映射分别映射到 8-bit 数据的 min/max。

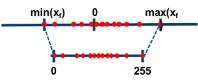
图1. 非对称算法示意图

如果我们用 x_f 表示 原始浮点数张量, 用 x_q 表示量化张量, 用 q_x 表示 scale，用 zp_x 表示 zero_point, n 表示量化数值的 bit数，这里 n=8， 那么非对称算法的量化公式如下：

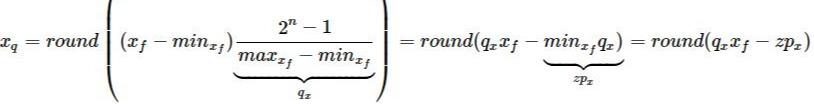
公式1. 非对称算法公式

上述公式中引入了 zero_point 的概念。它通常是一个整数，即 zp_x= rounding(q_x * min_x_f)。因此，在量化之后，浮点数中的 0 刚好对应这个整数。这也意味着 zero_point 可以无误差地量化浮点数中的数据 0，从而减少补零操作(比如卷积中的padding zero)在量化中产生额外的误差【3,4】。

但是，从上述公式我们可以发现 x_q 的结果只能是一个非负数，这也意味着其无法合理地处理有符号的 int8 量化，Pytorch 的处理措施是将零点向左移动 -128，并限制其在 [-128,127] 之间【5】。

• 对称算法(symmetric)

对称算法的基本思路是通过一个收缩因子(scale)将 FP32 tensor 中的最大绝对值映射到 8-bit数据的最大值，将最大绝对值的负值映射到 8-bit 数据的最小值。以 int8 为例，max(|x_f|)被映射到 127，-max(|x_f|)被映射到-128。 如下图所示：

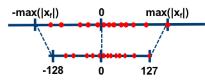
图2. 对称算法示意图

与非对称算法相比，对象算法一般不采用 zero_point, 其量化公式如下：

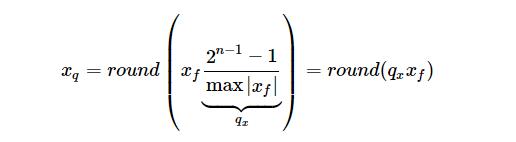
公式2. 对称算法公式

如果 FP32 张量的值能够大致均匀分布在 0 的左右，这种算法将数值映射到 int8 数据之后也能均匀的分布在 [-128, 127]之间。 但是对于分布不均与的 FP32 张量，量化之后将不能够充分利用 8-bit 的数据表示能力。

• 对称算法 VS 非对称的算法

非对称算法一般能够较好地处理数据分布不均与的情况，为了验证这个问题，我们用 python 做了一个小实验。FP32 原始数据均匀分布在 [-20, 1000]，这也意味着数据分布明显倾向于正数一方。下图展示了实验结果。从图中可以看出，对于这种FP32 数据分布不均匀的情况下，对称算法的量化数据分布与原始数据分布相差很大。由对称算法(symmetric)产生的 量化数据绝大部分都位于[0,127] 这个表示范围内，而 0 的左侧有相当于一部分范围内没有任何的数据。int8 本来在数据的表示范围上就明显少于 FP32，现在又有一部分表示范围没发挥左右，这将进一步减弱量化数据的表示能力，影响量化模型的精度。与之相反，非对称算法(asymmetric)则能较好地解决 FP32 数据分布不明显倾向于一侧的问题，量化数据的分布与原始数据分布情况大致相似，较好地保留了 FP32 数据信息。

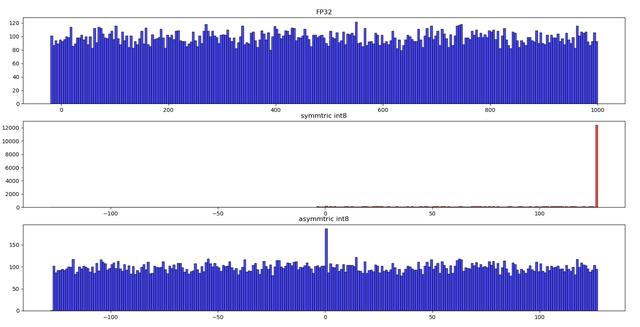
图3. 对称算法 VS 非对称算法

• 引入 zero-point 对算子的影响

卷积(convolution(Conv))和全连接(fully-connected (FC))中的主要操作都是乘加。为了简化问题说明，我们这里将其具体实现形式简化成乘加。以 y_