直线生成算法总结

最新推荐文章于 2023-03-16 02:21:19 发布

原创最新推荐文章于 2023-03-16 02:21:19 发布 · 2.6k 阅读

2 ·

CC 4.0 BY-SA版权

OpenGL 专栏收录该内容

12 篇文章

订阅专栏

1.DDA算法

void f(float x0,float y0,float x1,float y1)
{
	int length;
	if (abs(x1 - x0) <= abs(y1 - y0))
		length = abs(y1 - y0);
	else
		length = abs(x1 - x0);
	float dx = (x1 - x0) / length, dy = (y1 - y0) / length,
		x = x0 + 0.5, y = y0 + 0.5;
	glBegin(GL_POINTS);
	for (unsigned i = 1; i <= length; i++)
	{
		glVertex2i(x, y);
		x += dx;
		y += dy;
	}
	glEnd();
}

DDA算法的缺点在与除法运算，优点是每个坐标点只出现一次。

而DDA算法的特点是当直线与坐标轴越逼近，则阶梯状越明显，但间隔越长。这是由于|k|越小，则坐标值+1的间隔越长，假设k=0.3，那么最坏情况x轴间隔四个像素，而y轴只间隔一个像素。

这是100，100 400，110两个端点用DDA算法实现的直线，明显看到k|=0.25时阶梯状十分明显。

2.对称DDA算法

对称DDA算法是DDA算法的改进，基本思想是利用位移求点，x，y的解为

$x(n)=x(n-1)+\Delta x/\Delta n$

$y(n)=y(n-1)+\Delta y/\Delta n$

$1/2<=Max(\Delta x/\Delta n,\Delta x/\Delta n)<1$

利用移位计算 $\Delta n$ ，可以消除除法运算，提高效率，

但同一坐标点可能出现两次。

3.Bresenham算法

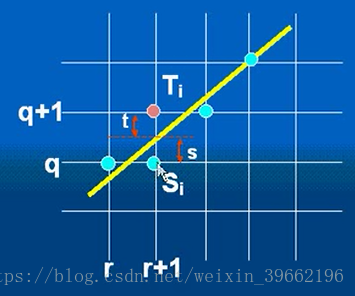
将直线移到原点

$s=\Delta y/\Delta x*(r+1)-q$

$t=(q+1)-\Delta y/\Delta x*(r+1)$

$\Delta x(s-t)=2(r\Delta y-q\Delta x)+2\Delta y-\Delta x(\Delta x>0)$

因此只要判断 $\Delta x(s-t)$ 的符号就可以确定下一点的坐标是Si还是Ti

令 $d_i=\Delta x(s-t)$ ,

当 $r=x_i_-_1,q=y_i_-_1$ 时，

$d_i=2x_i_-_1\Delta y-2y_i_-_1\Delta x+2\Delta y-\Delta x$

$d_i_+_1=2x_i\Delta y-2y_i\Delta x+2\Delta y-\Delta x$

$d_i_+_1=d_i+2\Delta y(x_i-x_i_-_1)-2\Delta x(y_i-y_i_-_1)$

因此， $d_i$ 的递推公式为：

$d_i_+_1=d_i+2\Delta y (d_i<0)$

$d_i_+_1=d_i+2\Delta y-2\Delta x (d_i>=0)$

$d_1=2\Delta y-\Delta x(i=0)$

当d>=0则取点t，否则取点s

void f(float x0,float y0,float x1,float y1)//0<=k<=1
{
	float dx = abs(x1 - x0), dy = abs(y1 - y0);
	float d = 2 * dy - dx, incr1 = 2 * dy,
		incr2 = 2 * (dy - dx);
	float x, y, xe, ye;//起点与终点
	if (x0 > x1) {
		x = x1; y = y1;
		xe = x0, ye = y0;
	}else {
		x = x0; y = y0;
		xe = x1; ye = y1;
	}
	//平移到原点
	float tx = x, ty = y;
	xe -= x, ye -= y;
	x = 0, y = 0;

	glBegin(GL_POINTS);
	glVertex2i(tx, ty); 
	while (x < xe)
	{
		x++;
		if (d < 0)d = d + incr1;
		else {
			y++;
			d = d + incr2;
		}
		glVertex2i(x + tx, y + ty);
	}
	glEnd();
}

Bresenham算法的优点在于只有加减运算，且每个坐标点只出现一次。

直线生成算法的共同点都是越逼近坐标轴，锯齿效果越明显，因此在大部分场合都需要使用抗锯齿的算法。