直线的生成的两种算法

1 DDA算法(数字微分分析法):

1.1算法思想:

从直线段的起点像素出发,依据直线的微分方程确定描述直线的各个像素点

1.2 算法原理:

直线的起点(xs,ys)

终点:(xe,ye)

变化量为cx=xe-xs,cy=ye-ys;我们将变化时间设为ct.

则有:

    x[i+1]=x[i]+cx/ct;

    y[i+1]=y[i]+cy/ct;

1.3 算法描述:

void drawline(int xs,ys,xe,ye)
{
    int k,i,x,y,dx,dy;
    k=abs(xe-xs);
    if(k<abs(ye-ys))
    {
        k=abs(ye-ys);//求最大值
    }
    dx=(xe-xs)/k;
    dy=(ye-ys)/k;
    x=xs;
    y=ys;
    for(i=0;i<k;i++)
    {
        plot(x,y);//画点
        x=x+dx;//下一个像素点
        y=y+dy;
    }
}

算法特点:

原理简单很容易实现,但是计算取整的积累会使得线段和理想的线段有所偏差:

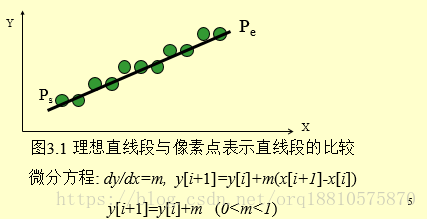
2 Bresenham算法:

2.1 算法思想

    根据直线的斜率确定选择x或y方向作为计长方向在这个方向上每次递增一个单位,另一个单位通过比较来确定是否增加一个单位

2.2 算法原理:

在斜率为0~1的1条件下,假设咱们选择以x轴为计长方向,p(xi,yi)是已经选定的距离直线最近的像素,现在要决定pi+1是选择T还是s.

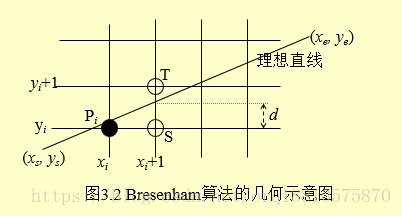
显然,要是e=d-0.5<0,则Pi+1(xi+1,yi)

否则Pi+1(xi+1,yi+1);

为了简便计算,咱们将e替换为:

e=2edx;

然后咱们得出递推公式:

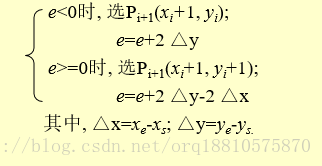
3 算法描述:

void drawline(int xs,ys,xe,ye)
{
    int i,x,y,dx,dy,e;
    dx=xe-xs;
    dy=ye-ys;
    e=-dx;
    x=xs;
    y=ys;
    for(i=0;i<dx;i++)
    {
        plot(x,y);
    }
    if(e>0)
    {
        y=y+1;
        e=e-2*dx;
    }
    x=x+1;
    e=e+2*dx;
}