支持向量机的基本思想_支持向量机学习（一）-优快云博客

支持向量机（SVM）旨在找到最优超平面，最大化两类样本间距离。其核心是确保样本中最接近超平面的支持向量与该平面保持足够大的间隔。SVM数学模型的建立涉及函数间隔和几何间隔的概念，以及通过拉格朗日乘子法解决约束优化问题，最终确定分类超平面。在实际应用中，当数据线性不可分时，SVM会有相应的处理策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

支持向量机的模型思想

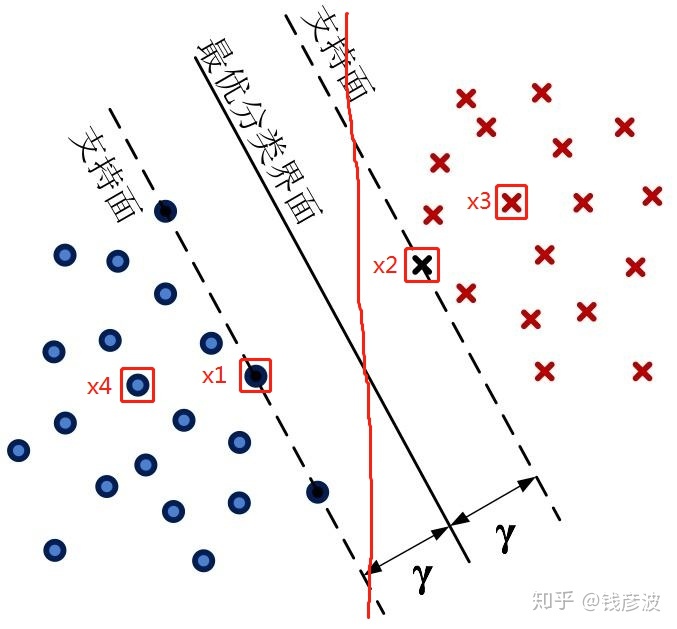
支持向量机从模型的思想上来说并不难理解，如下图所示，平面中有两种类型的点，一种是红色的X点，一种是蓝色的原点。我们现在要将这两种类型的点分开，存在这多种划分方法，我们可以从两类样本的中间化一条红色的直线（线画的不好，不要介意），但是我们会发现两类样本点离分界线都很近，这样如果我们新输入一个样本点，可能会造成分错类的现象，所以我们的分界线不能随意的取。我们要取一条最优的分界线，既能把两类样本点分开，而且还要使得两类样本点中离分界线最近的点离分界线的距离尽可能的远。这句话可能比较拗口，我们结合图像来说一下。如下图中我们圈起来的四个点x1，x2，x3，x4，我们在选取最优的分界线的时候，我们不可能去考虑x3和x4两个点，因为两个点之前的距离太大了，即使我们选取了分界线把这两个点很好的分开，但是不一定能把离得比较近的两类点分开。所以我们应该考虑两类点中离得最近的点，一方面只要保证这些点分开，那么其他离得远的点也很容易分开；另一方面，为了使分类的效果尽可能的好，我们又要保证这些最近的点离分界线的距离尽可能的远，如图中的x1，x2两点，是离得比较近的点，如果我们以红色的线作为分界面，那么样本点x1，x2到分界线的距离明显要小于x1，x2到图中最优分界线的距离。所以我们的目标就是找到如图中最有分界线这样的一条分界线。

对于在高维空间中，不像在二维空间中是一条直线，我们把高维空间中类似于二维空间中的分界线叫做超平面。另外我们也可以看到，虽然两类样本点都有很多点，但是真正其到作用的是那些离得比较近的点，他们位于超平面上，由于这些点真正的起到了决定分割超平面的作用，所有我们把这些点叫做支持向量。