正交投影矩阵_3D数学-正交投影

3D数学-正交投影

好记性不如烂笔头啊，还是记录一下!

---

概述

正交投影也被称为平行投影，不会出现透视投影的近大远小的扭曲现象，

---

正交投影的推导

构建正交投影矩阵相对来说会简单一些，由于不存在透视扭曲。

规范化设备坐标系（Normalized Device Coordinates）中的坐标

表示

近裁剪平面（near clip plane）的左边，即

表示

近裁剪平面（near clip plane）的右边，即

表示

近裁剪平面（near clip plane）的上边，即

表示

近裁剪平面（near clip plane）的下边，即

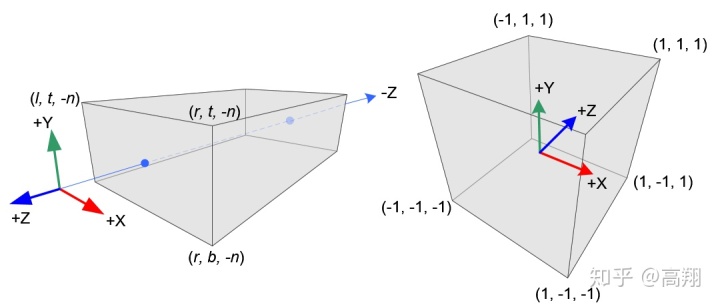
如图所示，

规范化设备坐标系（Normalized Device Coordinates）中的，因为我们实际只是将一个长方体缩成一个立方体，并把它移动到原点。下面我们就来使用

线性映射关系（linear relationship）来推导正交投影矩阵

现在需要将

映射到

，

得范围是

，

的范围是

，还需要将

映射到

，

得范围是

，

的范围是

，还需要将

映射到

，由于齐次裁剪空间为左手坐标系，所以需要将z轴反置，因此

的范围是

，

得范围是

可以利用简单线性插值的方法获得以下关系式：

解出可得：

将以上三个关系式写成矩阵形式，可得：

就是

正交投影矩阵

---

投影矩阵的另一种形式

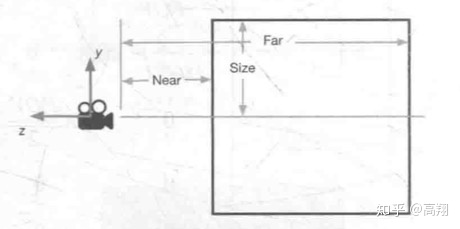
根据Size（竖直方向上高度的一半）和Aspect（投影平面的宽高比）可得出以下关系：

所以

还可以写成：

本节教程就到此结束,希望大家继续阅读我之后的教程。

谢谢大家,再见!

---

饮水思源

参考文献：

《3D游戏与图形学中的数学方法》

lxycg：OpenGL投影矩阵(Projection Matrix)构造方法​zhuanlan.zhihu.com

---

版权声明：原创技术文章，撰写不易，转载请注明出处！