线性调频信号_非平稳信号分析——调频调幅信号分析

最新推荐文章于 2024-05-04 19:12:29 发布

weixin_39641103

最新推荐文章于 2024-05-04 19:12:29 发布

阅读量1.2k

点赞数

CC 4.0 BY-SA版权

文章标签：线性调频信号

本文链接：https://blog.youkuaiyun.com/weixin_39641103/article/details/111579591

本文分析了调频调幅信号，包括STFT、Wigner-Ville分布和小波变换的效果。尽管这些方法能识别130Hz分量，但对基频为60Hz、调频频率为15Hz的调频成分分析不足。通过使用EMD分解和Hilbert谱分析，能够更准确地捕捉到信号的频率随时间变化的特征，揭示了调频调幅信号的真实结构。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

3.4调频调幅信号分析

调频调幅信号是实际应用中经常碰到的信号。通信信号是将所需传输的信息对载波进行调制，最常用的载波为连续正弦波，分析一调频调幅信号，其表达式为：

石显：非平稳信号HHT分析—跳频信号分析zhuanlan.zhihu.com

（3.1）

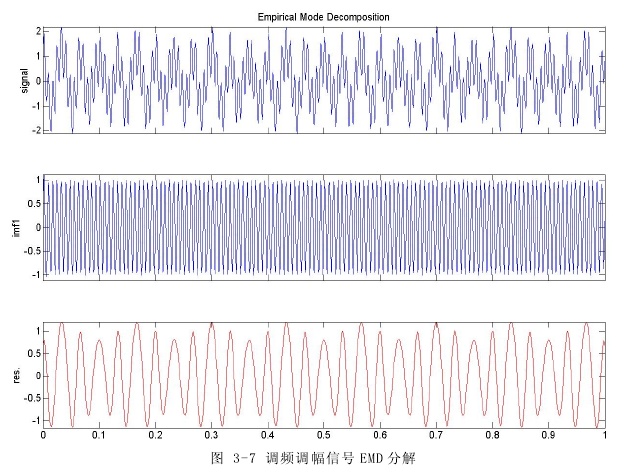
该信号由一个基频为30Hz，调频频率为15Hz的调频波和一个频率为130 Hz的正弦波组成。其时域波形如图3-7所示，时间t取0-1s，采样频率为1000Hz。这是一个包含两个频率分量的非线性信号。

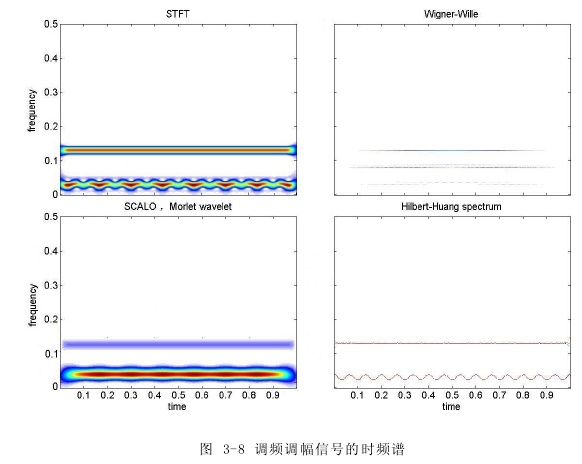
对该信号分别做 STFT、Wigner-Ville 分布和小波变换，其中小波变换选用 Morlet小波基。其处理结果如图3-8所示。

从这几幅时频谱图中我们可以观察到：三种方法能够分辨出频率为130Hz的正弦分量。短时傅立叶变换的频率分辨率较差；与窗函数的选择有关，而对于基频60Hz，调频频率为15Hz的调频分量，由于其时频分辨率不能兼顾的缺陷，只能看到频率、能量略有波动，但不清晰。Wigner-Ville分布可以看到两个频率分量，却依然存在交叉项的严重干扰，频谱中多出了不该有的频率成分，可读性较差。小波变换同样没有分辨出调频分量。

下面对式(3.1)的信号进行HHT分析。首先对信号进行EMD分解，分解后的imf分量及残余量如图3-7所示。EMD方法与其它的时频分析方法不同，其它的时频分析方法最终都是以傅立叶变换为基础的，而EMD分析方法以信号本身为特征尺度进行分解，分解出来的imf分量更真实地表征了原信号中的频率特征，具有自适应性。它先把频率最高的分量分解出来，imf1分量对应信号中130Hz频率的正弦波，res的波形幅值和间距都有变化，对应仿真信号的调频调幅分量。

对经EMD分解得到的imf分量进行Hilbert谱分析，得到原信号的Hilbert时频谱如图3-8。从该图看出，频率随时间的变化符合原信号的物理意义，有两个频率成分，一个是130Hz随时间不变的，另一个是围绕30Hz频率随时间成正弦波动的分量。由以上分析可知，Hilbert 谱提取到了原信号的频率组成及其与时间的关系的特征信息。