
堆的定义及其实现
• 最小堆:最小堆是一个关键码序列
{ K0,K1,…Kn-1},它具有如下特性:
•
•

类似可以定义最大堆
堆的性质
• 完全二叉树的层次序列,可以用数组表示
• 堆中储存的数是局部有序的,堆不唯一
• 结点的值与其孩子的值之间存在限制
• 任何一个结点与其兄弟之间都没有直接的限制
• 从逻辑角度看,堆实际上是一种树形结构
堆的类定义
template<class T>
class MinHeap{ // 最小堆ADT定义 堆的类定义
private:
T* heapArray; // 存放堆数据的数组
int CurrentSize; // 当前堆中元素数目
int MaxSize; // 堆所能容纳的最大元素数目
void BuildHeap(); // 建堆
public:
MinHeap(const int n); // 构造函数,n为最大元素数目
virtual ~MinHeap(){delete []heapArray;}; // 析构函数
bool isLeaf(int pos) const; // 如果是叶结点,返回TRUE
int leftchild(int pos) const; // 返回左孩子位置
int rightchild(int pos) const; // 返回右孩子位置
int parent(int pos) const; // 返回父结点位置
bool Remove(int pos, T& node); // 删除给定下标的元素
bool Insert(const T& newNode); // 向堆中插入新元素newNode
T& RemoveMin(); // 从堆顶删除最小值
void SiftUp(int position); // 从position向上开始调整,使序列成为堆
void SiftDown(int left); // 筛选法函数,参数left表示开始处理的数组下标
}
对最小堆用筛选法 SiftDown 调整
template <class T>
void MinHeap<T>::SiftDown(int position) {
int i = position; // 标识父结点
int j = 2*i+1; // 标识关键值较小的子结点
Ttemp = heapArray[i]; // 保存父结点
while (j < CurrentSize) {
if((j < CurrentSize-1)&&
(heapArray[j] > heapArray[j+1]))
j++; // j指向数值较小的子结点
if (temp > heapArray[j]) {
heapArray[i] = heapArray[j];
i = j;
j = 2*j + 1; // 向下继续
}
else break;
}
heapArray[i]=temp;
}

对最小堆用筛选法 SiftUp 向上调整
template<class T>
void MinHeap<T>::SiftUp(int position) {
// 从position向上开始调整,使序列成为堆
int temppos=position;
// 不是父子结点直接swap
T temp=heapArray[temppos];
while((temppos>0) && (heapArray[parent(temppos)] > temp)) {
heapArray[temppos]=heapArray[parent(temppos)];
temppos=parent(temppos);
}
heapArray[temppos]=temp;// 找到最终位置
}
建最小堆过程
• 首先,将 n 个关键码放到一维数组中
• 整体不是最小堆
• 所有叶结点子树本身是堆
• 当 i ≥
• 从倒数第二层,i =
• 直到整个过程到达树根
• 整棵完全二叉树就成为一个堆

建最小堆过程示意图
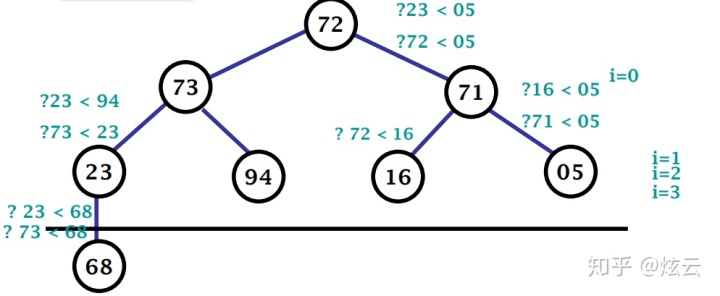
建最小堆
从第一个分支结点 heapArray[CurrentSize/2-1] 开始,自底向上逐步把以子树调整成堆
template<class T>
void MinHeap<T>::BuildHeap()
{
// 反复调用筛选函数
for (int i=CurrentSize/2-1; i>=0; i--)
SiftDown(i);
}
最小堆插入新元素
template <class T>
bool MinHeap<T>::Insert(const T& newNode)
//向堆中插入新元素newNode
{
if(CurrentSize==MaxSize) // 堆空间已经满
return false;
heapArray[CurrentSize]=newNode;
SiftUp(CurrentSize); // 向上调整
CurrentSize++;
}
最小堆删除元素操作
template<class T>
bool MinHeap<T>::Remove(int pos, T& node) {
if((pos<0)||(pos>=CurrentSize))
return false;
T temp=heapArray[pos];
heapArray[pos]=heapArray[--CurrentSize];
if (heapArray[parent(pos)]> heapArray[pos])
SiftUp(pos); //上升筛
else SiftDown(pos); // 向下筛
node=temp;
return true; }·
删除68
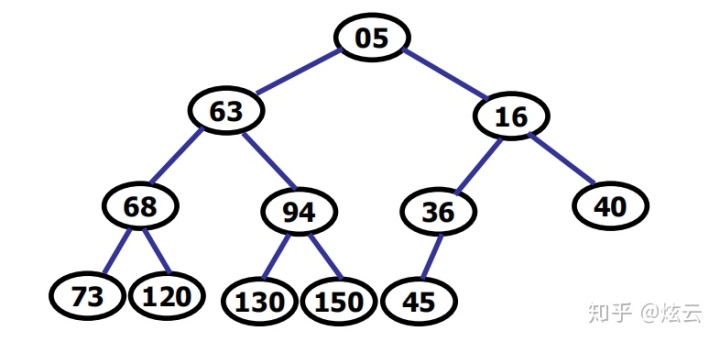
建堆效率分析
• n 个结点的堆,高度 d =
根为第 0 层,则第 i 层结点个数为
• 考虑一个元素在堆中向下移动的距离。
• 大约一半的结点深度为 d-1,不移动(叶)。
• 四分之一的结点深度为 d-2,而它们至多能向下移 动一层。
• 树中每向上一层,结点的数目为前一层的一半,而子树高度加一。因而元素移动的最大距离的总数为

最小堆操作效率• 建堆算法时间代价为 (n)
• 堆有 log n 层深
• 插入结点、删除普通元素和删除最小元素的平均
时间代价和最差时间代价都是
优先队列
• 堆可以用于实现优先队列
• 优先队列
• 根据需要释放具有最小(大)值的对象
• 最大树、 左高树HBLT、WBLT、MaxWBLT
• 改变已存储于优先队列中对象的优先权
• 辅助数据结构帮助找到对象
思考
• 在向下筛选SiftDown操作时,若一旦发现
逆序对,就交换会怎么样?
• 能否在一个数据结构中同时维护最大值和
最小值?(提示:最大最小堆)




 本文详细介绍了堆的定义、性质以及最小堆的构建过程,通过筛选法SiftDown和SiftUp进行调整。建堆效率分析表明,对于n个节点的堆,建堆的时间代价为O(n)。堆作为优先队列的数据结构,可以高效地实现插入、删除等操作。文章探讨了在筛选过程中逆序对的处理以及如何设计数据结构同时维护最大值和最小值。
本文详细介绍了堆的定义、性质以及最小堆的构建过程,通过筛选法SiftDown和SiftUp进行调整。建堆效率分析表明,对于n个节点的堆,建堆的时间代价为O(n)。堆作为优先队列的数据结构,可以高效地实现插入、删除等操作。文章探讨了在筛选过程中逆序对的处理以及如何设计数据结构同时维护最大值和最小值。
















 2670
2670

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








