数据结构visit函数_第10篇:C++ 数据结构-二叉树的遍历模式

二叉树的遍历方式

树的遍历操作：就是以特定的顺序访问树中每个节点的过程，通过查找树中特定的节点，以便执行修改、删除、或获取数据值。我们在前一篇实现BST的查找、插入算法，其实就伴随实现了某种遍历算法。

树并不像线性表那样遍历方式那么单一化，只有一个起始节点和结束节点就完事。从维度来理解，链表是一维的数据结构，树是一种二维的数据结构。可以理解树就是多个相关联的链表的超集。因为我们可以从任意一个非空节点沿着不同的方向遍历到叶子节点得到一个逻辑上的链表。

本篇需要实现的BST内部接口

template<class T>
class BSTree{
private:
    BNode<T>* d_root; //整个树的根
    int d_size;      //当前元素的高度
    ....
    
    //遍历某层的节点
    void level_visit(BNode<T>*,ArrayList<T>*,int);

    //先序遍历
    void pre_visit(BNode<T>*,ArrayList<T>*);
    
    //按序遍历
    void ord_visit(BNode<T>*,ArrayList<T>*);
    
    //后序遍历
    void post_visit(BNode<T>*,ArrayList<T>*);

public:
    BSTree();

    //构造函数
    BSTree(const T* arr,int size);

    //析构函数
    ~BSTree();
    ....
    //级别遍历
    ArrayList<T>* level_traversal(int);

    //后序遍历
    ArrayList<T>* post_traversal();

    //前序遍历
    ArrayList<T>* pre_traversal();

    //顺序遍历
    ArrayList<T>* order_traversal();

    template<typename R>
    friend std::ostream &operator<<(std::ostream &,const BSTree<R> &);

};

在树的遍历中，每当我们到达某个节点，都面临着遍历方向的决策问题。在二叉树中，按照节点的顺序，树的遍历方式大体上分为两种

广度优先遍历(Breath-first Traversal)和深度优先遍历(Depth-first Traversal).

广度优先遍历和深度优先遍历是遍历或搜索图的遍历方式，图是一种数据结构，目前我们还没有讨论图。现在我们只需知道树是图的一个子集，是一种特殊的图。

广度优先遍历

广度优先遍历的原则：以访问相同深度的所有节点为优先，换句话说按照

的遍历顺序。先遍历0层的所有节点、再遍历1层的所有节点....如此类推，如下图所示：

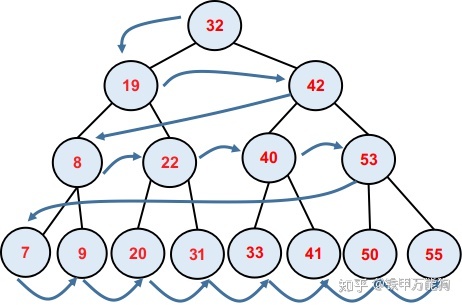
由于这种遍历方式从左到右，从低级别往高级别递增的访问的模式，也叫级别顺序遍历.

如果你对二叉堆还有印象的话，二叉堆的默认遍历方式就是级别顺序遍历，在泛指二叉树的情况下，该算法实现一般分为两种情况。

• 是获取所有层的节点值？本文定义算法的方法名为level_visit()
• 是获取某层的节点值?定义算法的方法名为level_visti(int)

下面的级别顺序遍历算法，我们使用了前面实现过的ArrayList顺序表来装载level_traversal方法返回的结果，ArrayList实现具体见《第1篇 C++ 数据结构--ArrayList的实现》

//公开的级别遍历方法
template<class T>
ArrayList<T>* BSTree<T>::level_traversal(int k){
    ArrayList<T>* arr=new ArrayList<T>();

    int height=maxHeight(d_root);

    if(k>height){
        delete arr;
        throw OperationException("传入的高度参数超入当前二叉树高度!!");
    }

    if(arr!=nullptr){
        level_visit(d_root,arr,k);
    }

    return arr;
}


//级别遍历的私有方法
template<class T>
void BSTree<T>::level_visit(BNode<T>* node,ArrayList<T> *res,int k){
    
    if(node==nullptr) return;

    if(k==0){
        res->push_back(node->d_data);
    }else if(k>=1){
        level_visit(node->d_left,res,k-1);
        level_visit(node->d_right,res,k-1);
    }
}

我们说，对于访问高度为n的BST，这种级别遍历算法最差的时间复杂度为

, 那么依次获取每层的所有节点，其时间复杂度

.

因此我们实现中如果要以级别顺序遍历并获取树中所有节点，最好的数据结构是二叉堆，因为二叉堆实现同样逻辑的二叉树，它最差的时间复杂度也稳定在

。因为二叉堆是基于线性表构建的。

深度优先遍历

在深度优先遍历的方式中，访问的相对顺序是首先是左子树、根节点、右子树，但没由硬性要求一定是这样的顺序，例如可以是右子树、根节点、左子树。

不过深度优先策略的决策思想是访问一个子树中的任意一个节点，是优先先向下一级子节点迭代还是优先提取该节点的数据值。我们用字母D表示读取或修改当前节点的数据，用字母L标识向左子树遍历，用字母R表示向向右子树遍历。LR的操作顺序在大多数情况下访问是相对固定的，也就是说基于操作D和和操作LR，深度优先遍历可以细分为三种遍历方式

• 前序遍历(Pre-Order)，简称DLR：先访问根节点->左子数->右子数。左子树和右子树是以相同的递归方式访问。
• 有序遍历(In-Order)，这里简称LDR：先访问根的左子树->根节点->根的右子树。
• 后序遍历(Post-Order)，这里简称LRD：先访问根左子树->根的右子树->根节点。

以上三种深度优先策略的遍历方式，左子树的顺序通常优先于右子树，换句话说上面三种遍历方式是以根节点的相对顺序变化分类的。

先序遍历(Pre-Order)

知乎视频​www.zhihu.com

实现该算法

//前序遍历的公开方法
template<class T>
ArrayList<T>* BSTree<T>::pre_traversal(){
    ArrayList<T>* arr=new ArrayList<T>();
    if(arr!=nullptr){
        pre_visit(d_root,arr);
    }
    return arr;
}

//前序遍历的私有方法
template<class T>
void BSTree<T>::pre_visit(BNode<T>* node,ArrayList<T>* arr){
    if(node==nullptr){
        return;
    }
    arr->push_back(node->d_data);
    pre_visit(node->d_left,arr);
    pre_visit(node->d_right,arr);
}

有序遍历(In-Order)

知乎视频​www.zhihu.com

实现该算法

//有序遍历
template<class T>
ArrayList<T>* BSTree<T>::order_traversal(){
    ArrayList<T>* arr=new ArrayList<T>();

    if(arr!=nullptr){
        ord_visit(d_root,arr);
    }
    return arr;
}

//有序遍历的私有方法
template<class T>
void BSTree<T>::ord_visit(BNode<T>* node,ArrayList<T>* arr){
    if(node==nullptr){
        return;
    }

    ord_visit(node->d_left,arr);
    arr->push_back(node->d_data);
    ord_visit(node->d_right,arr);
}

后序遍历(Post-Order)

知乎视频​www.zhihu.com

实现该算法

//后序遍历的公开版本
template<class T>
ArrayList<T>* BSTree<T>::post_traversal(){
    ArrayList<T>* arr=new ArrayList<T>();
    if(arr!=nullptr){
        post_visit(d_root,arr);
    }
    return arr;
}

//后序遍历的私有方法
template<class T>
void BSTree<T>::post_visit(BNode<T>* node,ArrayList<T>* arr){
    if(node==nullptr){
        return;
    }

    post_visit(node->d_left,arr);
    post_visit(node->d_right,arr);
    arr->push_back(node->d_data);
}

本篇算法API测试

#include <iostream>
#include "libs/BSTree.cpp"
int main()
{
    int arr[13]={32,19,42,8,22,40,53,7,9,20,31,41,55};
    BSTree<int>* b=new BSTree<int>(arr,13);
    std::cout<<"树高度:"<<b->height()<<std::endl;
    std::cout<<"节点个数:"<<b->size()<<std::endl;

    std::cout<<"最小值:"<<b->min()<<std::endl;
    std::cout<<"最大值:"<<b->max()<<std::endl;
    
    std::cout<<((b->find(30))?"found":"not found")<<std::endl;

    ArrayList<int>* m=b->level_traversal(3);
    std::cout<<"级别遍历:";
    std::cout<<*m<<std::endl;

    ArrayList<int>* m2=b->pre_traversal();
    std::cout<<"前序遍历:";
    std::cout<<*m2<<std::endl;

    ArrayList<int>* m3=b->order_traversal();
    std::cout<<"有序遍历:";
    std::cout<<*m3<<std::endl;

    ArrayList<int>* m4=b->post_traversal();
    std::cout<<"后序遍历:";
    std::cout<<*m4<<std::endl;

    delete m,m2,m3,m4;
    delete b;
    
    return 0;
}

调用示例如下图

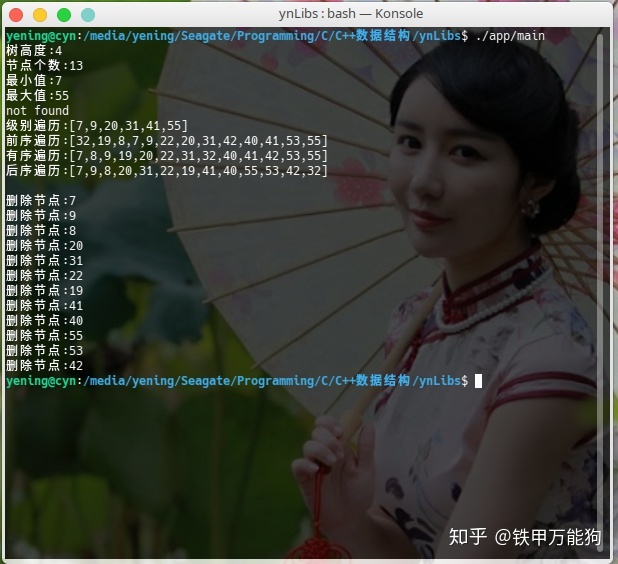
小结：

本篇我们用到了前面篇章的ArrayList来配合实现我们BST的常用且较为实用的遍历算法，写啥，现在没有心情写.....