plor 回归的r方_R相关与回归学习笔记（十六）——残差诊断（一）

本笔记中原始数据及代码均来源于李东风先生的R语言教程，在此对李东风先生的无私分享表示感谢。

先复习一些回归理论。 将模型写成矩阵形式

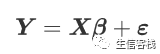
Y为n×1向量, X为n×p矩阵, 一般第一列元素全是1, 代表截距项。 β为p×1未知参数向量; ε为n×1随机误差向量, ε的元素独立且方差为相等的σ方(未知)。 假设矩阵满秩，系数的估计为

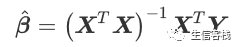
拟合值(或称预报值)向量为

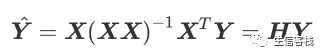
其中

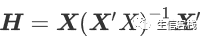
是Rn次方空间的向量向X的列张成的线性空间μ(X)投影的投影算子矩阵, 叫做帽子矩阵。 设

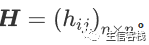
拟合残差向量为

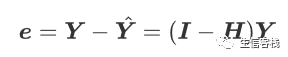
残差平方和为

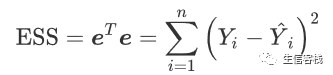
误差项方差的估计 (要求设计阵X满秩)为均方误差(MSE)

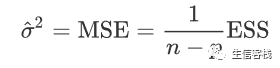
(其中p在有截距项时是自变量个数加1) 在线性模型的假设下, 若设计阵X满秩, β^和σ方^分别是β和σ方的无偏估计。 系数估计的方差阵

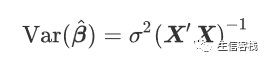
回归残差及其方差为

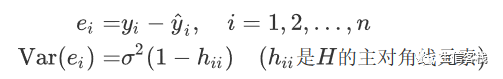
若lmres是R中lm()的回归结果， 用residuals(lmres)可以求残差。 把ei除以其标准差估计， 称为标准化残差，或内部学生化残差：

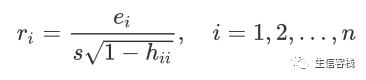
ri渐近服从正态分布。 若lmres是R中lm()的回归结果， 用rstandard(lmres)可以求标准化残差。 如果计算yi的预测值时， 删除第i个观测后建立回归模型得到σ方的估计s(i)方， 则外部学生化残差为

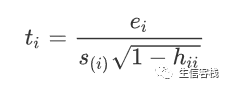
ti近似服从t(n-p-1)分布 (有截距项时p等于自变量个数加1)。 其中s(i)有简单公式：

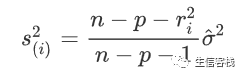
若lmres是R中lm()的回归结果， 用rstudent(lmres)可以求外部学生化残差。

往期回顾

R相关与回归学习笔记(一)——相关分析

R相关与回归学习笔记(二)——相关与因果、相关系数大小、相关系数的检验

R相关与回归学习笔记(三)——相关阵、一元回归分析

R相关与回归学习笔记(五)——回归有效性

R相关与回归学习笔记(六)——R程序

R相关与回归学习笔记(七)——回归诊断(一)

R相关与回归学习笔记(七)——回归诊断(二)

R相关与回归学习笔记(八)——回归诊断(三)

R相关与回归学习笔记(九)——预测区间、控制、多元线性回归模型

R相关与回归学习笔记(十)——参数估计、R的多元回归程序(一)

R相关与回归学习笔记(十一)——模型的检验

R相关与回归学习笔记(十二)——线性关系检验、单个斜率项的显著性检验

R相关与回归学习笔记(十三)——回归自变量筛选

R相关与回归学习笔记(十四)——哑变量与变截距项的模型(一)

R相关与回归学习笔记(十五)——哑变量与变截距项的模型(二)