k均值聚类算法优缺点_聚类算法之——二分K-Means算法

最新推荐文章于 2021-06-01 12:44:01 发布

最新推荐文章于 2021-06-01 12:44:01 发布 · 640 阅读

文章标签：

#k均值聚类算法优缺点

为解决K-Means算法易陷入局部最优的问题，本文介绍了一种改进算法——二分K-Means。该算法从所有数据点作为单一簇开始，通过反复将簇一分为二来逐步降低误差平方和(SSE)，直至达到指定的簇数量。

为克服K-Means算法收敛于局部最小值问题，提出了二分K-Means算法

二分K-Means算法首先将所有点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复，直到得到用户指定的簇数目为止。

步骤

1. 将所有点看成一个簇；

2. 对每个簇，进行如下操作

计算总误差

在给定的簇上进行K-Means聚类（k=2）

计算将该簇一分为二之后的总误差

3. 选择使得误差SSE最小的那个簇进行划分操作

4. 重复2—3操作，直到达到用户指定的簇数目为止；

另一种做法是：选择SSE最大的簇进行划分，直到簇数目达到用户指定的数目为止。

python代码

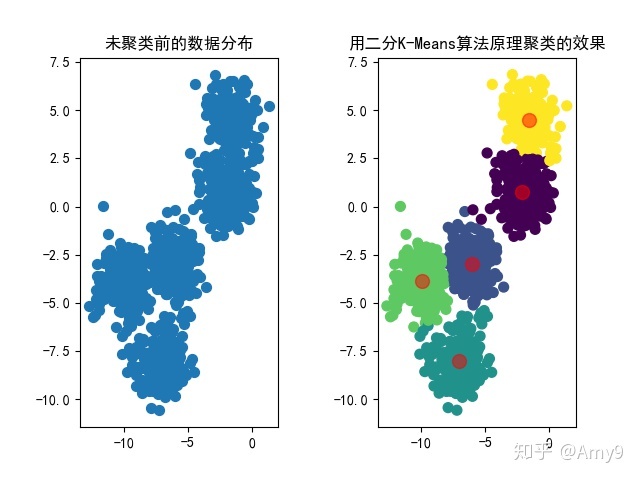
import

结果如下

相关链接

K-Means算法链接

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

weixin_39638708

关注关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

机器学习实战学习笔记 --- 二分K-Means聚类算法

杨鑫newlife的专栏

03-28

1049

K -Means聚类算法的缺陷在K-Means的函数测试中，可能会偶尔陷入局部最小值（局部最优的结果，但不是全局最优的结果）解决方案：为了克服K-Means算法收敛于局部最小值的问题，有一个好的解决方案是二分K-Mean(二分K均值 bisecting K-Means)的算法原理：该算法首选所有点作为一个簇，然后将该点一份为二。之后选择一个簇继续划分，选择哪一个簇进行...

机器学习（二）：二分K-means算法（进阶篇）

Auraros的博客

06-22

7398

机器学习（二）：二分K-means算法在前一节的内容已经介绍了k-means算法的原理和代码实现，如果没有了解过K-means的同学建议先了解机器学习（二）：k-means算法（基础篇）二分k-means是k-means算法的一种优化，二分k-means算法很好的解决了k-means算法的局部最优的问题。接下来我们来了解一下二分k-means的神奇之处二分k-means算法二分k-mean...

参与评论您还未登录，请先登录后发表或查看评论

K-Means算法及其变种，优缺点分析笔记

夏未眠秋风起的博客

10-03

2741

K-Mneans算法是常见，常用，常考的算法，因此这里做个笔记，多多复习。 k-means算法的主要流程 1.根据需求，初始化k个中心点 2.为每个样本点计算他们和k个中心点的距离，找到距离最近的中心点，即该样本就属于这个中心点所代表的的类 3.做完2后，就已经对样本做了一次分类了，接着计算每个类别中的样本点的均值，用这些均值代替原来的k个样本点。 4.重复2,3知道满足一些条件（迭代次数，误差大小等）。距离有多种计算方法：距离度量的不同方法可以参考我的另一篇博客https://blog.cs

二分K-means聚类，K-Means改进

skyonefly的博客

12-09

5062

由于K-means 有可能会收敛到局部最优值，而无法收敛到全局最优值，影响聚类性能一种用于度量聚类效果的指标是SSE(Sum of Squared Error，误差平方和），对应予 clusterAssment第二列此算法的思想是，为克服K-均值算法收敛于局部最小值，我们使用二分K-均值：先将所有点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于是

机器学习实战Chp10： K-均值聚类及改进的二分 K-均值算法

muli

08-01

644

机器学习实战Chp10： K-均值聚类及改进的二分 K-均值算法 # -*- coding: utf-8 -*- """ Created on Wed Aug 01 09:48:28 2018 @author: muli """ from numpy import * # 加载数据 def loadDataSet(fileName): #general function t..

精选资源

k-均值聚类算法实现灰度图像分割_K均值算法_K._图像聚类_图像聚类_图像分割_

10-04

k-均值聚类算法（K-Means Clustering）是一种广泛应用的数据分析方法，尤其在图像处理领域，常用于图像的灰度图像分割。该算法通过将数据集中的样本点分配到最近的聚类中心所属的类别，以此来达到划分的目的。在图像...

精选资源

粒子群_改进K均值聚类算法_matlab_k-means_pso_pso-clustering

03-11

资源名：粒子群_改进K均值聚类算法_matlab_k-means_pso_pso-clustering 资源类型：matlab项目全套源码源码说明：全部项目源码都是经过测试校正后百分百成功运行的，如果您下载后不能运行可联系我进行指导或者更换...

精选资源

K均值算法程序.rar_K-均值_K均值_K均值聚类算法_matlab_kjunzhi_聚类，分类

07-15

K均值（K-Means）算法是一种广泛应用的无监督机器学习方法，主要用于数据的聚类分析。在给定的数据集中，K均值算法通过迭代寻找最佳的类别划分，使得同一类别的样本间距离最小，不同类别间的样本距离最大。在本案例...

K-均值聚类_k均值聚类_K均值_K._k均值matlab_K均值聚类算法_

09-29

《K-均值聚类算法在Matlab中的实现》 K-均值聚类（K-Means Clustering）是一种广泛应用的数据分析方法，主要用于无监督学习中的数据分组。它通过迭代过程，将数据集中的样本点分配到最近的聚类中心所属的簇中，以...

一种新的聚类分析距离算法.rar_K-means 聚类算法_K均值聚类数_k-means聚类算法

09-23

标签中的“k均值聚类数”指的是k值的选择，它是K-means算法的关键参数。常见的确定k值的方法有肘部法则（Elbow Method）、轮廓系数（Silhouette Coefficient）等。肘部法则通过绘制不同k值下的误差平方和（SSE）与k...

二分k-means

weixin_41690708的博客

07-10

888

由于K-Means对于初始簇心比较敏感，解决K-Means算法对初始簇心比较敏感的问题，二分K-Means算法是一种弱化初始质心的一种算法，具体思路步骤如下： 1、将所有样本数据作为一个簇放到一个队列中从队列中选择一个簇进行K-means算法划分，划分为两个子簇，并将子簇添加到队列中 2、循环迭代第二步操作，直到中止条件达到(聚簇数量、最小平方误差、迭代次数等) 队列中的簇就是最终的分类簇集合...

聚类练习：对地理数据应用二分k-均值算法聚类

Yuetian_w的博客

06-01

1480

文章目录**编程作业：聚类**实验原理：k-means聚类：二分k-means聚类：使用后处理来提高聚类性能：任务：对地理数据应用二分k-均值算法聚类（1）问题描述：（2）具体实现：（3）实验结果：实验小结：编程作业：聚类实验原理：参考：机器学习实战 (豆瓣) (douban.com) (13条消息) 机器学习实战第十章利用K-均值聚类算法对未标注数据分组_无名的博客-优快云博客 k-means聚类： k-means聚类将相似的对象归到同一个簇中，每个簇的中心采用簇中所含值的均值计算而成。优

k均值聚类算法优缺点_机器学习实战项目- K-Means（K-均值）聚类算法

weixin_39527487的博客

11-29

1328

K-Means 算法聚类是一种无监督的学习, 它将相似的对象归到一个簇中, 将不相似对象归到不同簇中.相似这一概念取决于所选择的相似度计算方法.K-Means 是发现给定数据集的 K 个簇的聚类算法, 之所以称之为 K-均值是因为它可以发现 K 个不同的簇, 且每个簇的中心采用簇中所含值的均值计算而成.簇个数 K 是用户指定的, 每一个簇通过其质心(centroid), 即簇中所有点的中心来描述...

聚类算法 - K-Means、二分K-Means、K-Means 、K-Means||、Canopy、Mini Batch K-Means算法

qfikh的博客

04-14

3555

K-Means 系列：K-Means，二分K-Means，K-Means++，K-Meansll，canopy算法，MiniBatchK-Means算法。 K-Means系列聚类算法原理：https://www.cnblogs.com/pinard/p/6164214.html 用scikit-learn学习K-Means聚类：https://www.cnblogs.com/pinar...

k-means和二分k-means算法

waeceo的专栏

06-27

2636

聚类算法是机器学习中的一类无监督学习方法，用于将无标签的数据进行聚类划分。最简单的也最典型的一类算法就是KMeans算法。此处的K表示划分成K个聚类。利用各个点到质心之间的距离的平方和作为将节点划分到不同类的标准。当然也可以采用其他的距离计算方法，不一定是欧式距离方法。一、KMeans 此方法一般是在数据分析前期使用，选取适当的K，将数据聚类后，研究不同聚类下数据的特点。算法原理：（...

聚类算法（K-means）

咔咔响

01-09

1437

1.聚类，通俗解释就是物以类聚2.聚类算法没有训练过程，这是和分类算法最本质的区别3.K-means是一种最常见的聚类算法，它通过距离定义相似性4.求解K-means采取启发式的迭代方法...

K-means 算法 Kmeans++ 二分Kmeans

promisejia

03-09

2072

1. 算法原理 kmeans的计算方法如下：随机选取k个中心点遍历所有数据，将每个数据划分到最近的中心点中计算每个聚类的平均值，并作为新的中心点重复 2-3 ，直到这k个中线点不再变化（收敛了），或执行了足够多的迭代或最小化平方误差。 2. 最小化平方误差法 3. kmeans的优缺点 4. 代码 ...

二分K-means算法

weixin_30549657的博客

11-29

394

二分K-means聚类（bisecting K-means）算法优缺点：由于这个是K-means的改进算法，所以优缺点与之相同。算法思想： 1.要了解这个首先应该了解K-means算法，可以看这里这个算法的思想是：首先将所有点作为一个簇，然后将该簇一分为二。之后选择能最大程度降低聚类代价函数（也就是误差平方和）的簇划分为两个簇（或者选择最大的簇等，选择方法多种）。以此进行下去...