标准正态分布_正态分布，正态分布如何变换为标准正态分布

正态分布（Normal distribution），又名高斯分布（Gaussian distribution）

若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0, σ = 1时的正态分布是标准正态分布。

一维正态分布的概率密度函数为

正太分布 变换 标准正太分布（均值为0，标准差为1）

其中

为正太分布分均值，

为正太分布的标准差，z为变化后的值。X为随意变量。

例如：2，3，4的均值为3，方差为

，标准差为

。

进行标准正太分布后，随机变量变为

，0，

，然后求均值为0，方差为1。

正态分布的一些性质：

（1）如果

且a与b是实数，那么

（2）如果

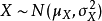
与

是统计独立的正态随机变量，那么：

它们的和也满足正态分布

它们的差也满足正态分布

U与V两者是相互独立的。（要求X与Y的方差相等）。

期望和方差的性质：

双木止月Tong：【“数”你好看】期望E(X)与方差Var(X)​zhuanlan.zhihu.com