一、简单理解卷积的概念
1.1卷积的定义:
定义任意两个信号的卷积为
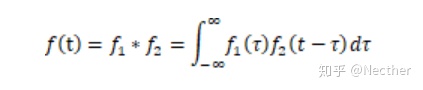
这里的*代表卷积的运算符号, 是中间变量,两个信号的卷积仍是以t为变量的信号。
类似地,离散的信号的卷积和:
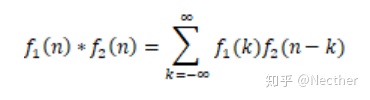
1.2 卷积的计算步骤:
(1)将上面的 、 中的自变量t换为 ,得到 、 ;
(2)将函数 以纵坐标为轴折叠,得到折叠信号 ;
(3)将折叠信号 沿 轴平移t,t为变量,从而得到平移信号 ,t<0时左移,t>0时右移;
(4)将 与 相乘,得到相乘信号 的非零区间,从而确定卷积积分的上下限,随着t的变化,积分限也会变化;
(5)计算函数 的曲线下的面积。
深度学习本质上是通过两大算子,解决了特征提取的问题。一个是卷积算子,一个是循环网络的一系列算子。卷积解决空间上的关系问题,循环解决时间上的关系问题。
但是卷积早已有之,本文主要解释卷积的工作原理和作用。
视觉辨别一个事物,最重要的因素是感知边缘。
比如眼前是一片黑,没有一点起伏,也就是相邻像素数字没有一点变化,那就没有信息了。所以要识别图像中的信息就要有办法可以把边缘信息给提取出来。卷积算子就是为此而设计。
最简单的卷积如下:
|-1|0|1|
|-|-|-|
假如有个图片
|1|1|5|1|1|
|1|1|5|1|1|
|1|1|5|1|1|
中间的这个5的地方就是一个边缘,如果我们将上面的卷积核 和该图片做卷积运算 也就是对位相乘然后相加,就会发现运动到5这个地方的时候出现变化,因为如果整片图片都是相同的数字,-1和1的结果相加总是等于0.所以我们通过卷积运算得到了边缘信息。
人们发现有这样一个运算方法可以得到图像的边缘信息的时候,就开始设计各种各样的卷积核用于检测图像的边缘。常见的有索贝尔算子、拉普拉斯算子。
这是在没有深度学习的时代的图像特征提取方法,我们把这一系列的算子提取的特征叫做本地特征,也就是这个特征是通过人为设计卷积核计算出来的。
到了有深度学习的时代,卷积核里面的参数就不是人为设计的了,变成了靠深度网络的优化器 通过反向传播算法来学习调整卷积核里面的参数。
可以参考下面的链接中的文章
Convolutional Neural Networks - Basics
在面试中经常问的一个问题是:
一个10*10的三通道图 3*3的卷积核 6个卷积核 有多少个参数?
根据上面的对位相乘再相加的原理可得 每个核要去和一个三通道*3*3的位置对位相乘 需要二十七个参数 加上一个偏置项 也就是28个 总共有六个核 所以是28*6的参数
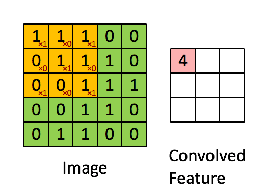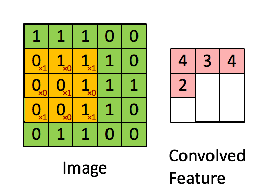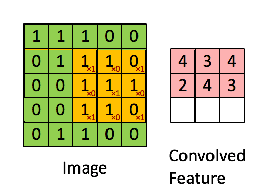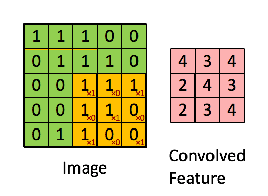






 本文解析卷积的基本概念,阐述其如何通过边缘检测揭示图像信息,从传统特征提取到深度学习时代的参数学习。讨论了3*3卷积核在10*10图像上的参数计算,并涉及卷积在视觉识别中的核心作用。
本文解析卷积的基本概念,阐述其如何通过边缘检测揭示图像信息,从传统特征提取到深度学习时代的参数学习。讨论了3*3卷积核在10*10图像上的参数计算,并涉及卷积在视觉识别中的核心作用。
















 780
780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








