正态分布表怎么查表_正态分布的运用

上一篇文章介绍了正态分布的计算，可参考：逆流：正态分布

本文介绍正态分布计算的几种运用情况。

假设要设计一个双人秋千，秋千的承载最多380斤的重量，小明和小红要同时坐上秋千，已知小明和小红的体重概率分布为N(150,400)、N(190,500)，求两人体重不超过秋千承载量的概率是多少？

小明+小红的体重之和的概率分布是多少？

在离散数据中，我们知道如何计算两个独立变量X、Y和的期望和方差，而这些计算方法同样是适用于连续数据的。

E(X+Y)=E(X)+E(Y)

Var(X+Y) = Var(X)+Var(Y)

如果把小明和小红的体重看作独立随机变量X，Y，则可写作：

其中

（1）所以小明和小红的综合体重分布为 X+Y~N(150+190，400+500)

（2）求综合体重少于380磅的概率

求标准分Z

Z = 380-μ / σ

= 380-340/30

=1.33

查Z表

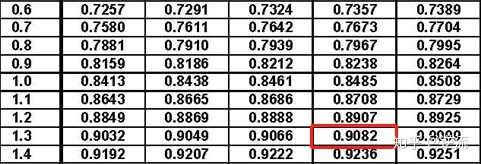
P(X+Y<380) =0.9082

练习题：

已知两名男女相亲，身高以英寸计数，男性身高的概率分布为X~N(71,20.25)，女性身高概率分布为Y~N(64,16)，求男子比女子高5英寸的概率是多少？

先求出X-Y的概率分布

E(X-Y)=E(X)-E(Y)

Var(X-Y) = Var(X)+Var(Y)

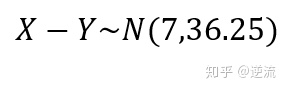
求标准分Z

Z = 5 - 7 / 6.02 = -0.33

查Z表

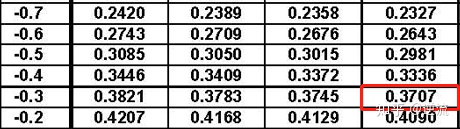
P(X-Y<5) = 0.3707

P(X-Y>5) = 1-P(X-Y<5) = 1-0.3707 =0.6293

正态分布的独立观察结果与线性变换

【独立观察结果】

根据上面的例子，进一步深入，假设我们要求4个小明的综合体重的概率分布。

则是求

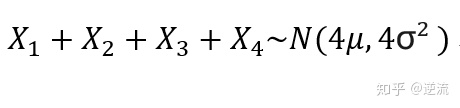
这称之为独立观察结果，总结公式为：

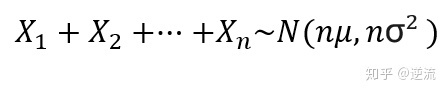
【线性变换】

假设我们要求的是1个小明的体重概率分布，但小明胖了，体重增加4倍。

通过E(X)和Var(X)的线性变化公式

E(aX+b) = aE(X)+b

Var(aX+b) =a²Var(X)

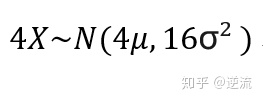
总结公式：

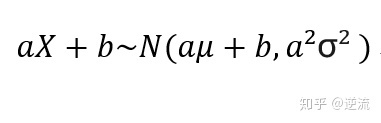
练习题：假定每个成年人的体重分布都符合N（180，625）,4个成年人的综合体重小于800磅的概率是多少？如果来了一个大胖子，体重分布是一般成年人体重的4倍，他的体重大于800磅的概率是多少？

（1）

X1+X2+X3+X4~N(720,2500)

求标准分

Z = 800-720/50 =1.6

查Z表

P（X1+X2+X3+X4<800）= 0.9452

所以4个成年人的综合体重小于800磅的概率是0.9452

（2）

4X~N（720,10000）

求标准分

Z=800-720 / 100 =0.8

查Z表

P（4X<800）=0.7881

P（4X>800）=1-0.7881 =0.2119

所以胖子的体重大于800磅的概率是0.2119

正态分布近似代替二项式分布

假设我们参加智力答题比赛，每道题目由4个选项组成，因此每题答对的概率为0.25，答错概率为0.75，总共有40道题，你答对30道题才能进入下一轮比赛，那么你晋级的概率是多少？

这道题如果用二项式分布计算，则我们必须将P(X=30)——P(X=40)的11个概率全部算出来再加总，这是一个非常庞大的计算量，计算过程极容易出错，而需要一个更简便的计算方法。

什么时候可以用正态分布近似代替二项式分布？

如果X~B（n,p）,且np>5,nq>5，则可以使用X~N(np,npq)近似代替二项式分布

注意：因为二项式分布式是离散分布，正太分布是连续分布，两者之间概率范围是存在差异的，所以不能直接将计算结果作为近似估计。还需要进行连续性修正。

连续性修正

【1】≤型概率求解

计算P(X≤a)这种形式的概率时，要确保所选择范围包含离散数值a，在一个连续标度上，离散数值a会增长到（a+0.5）

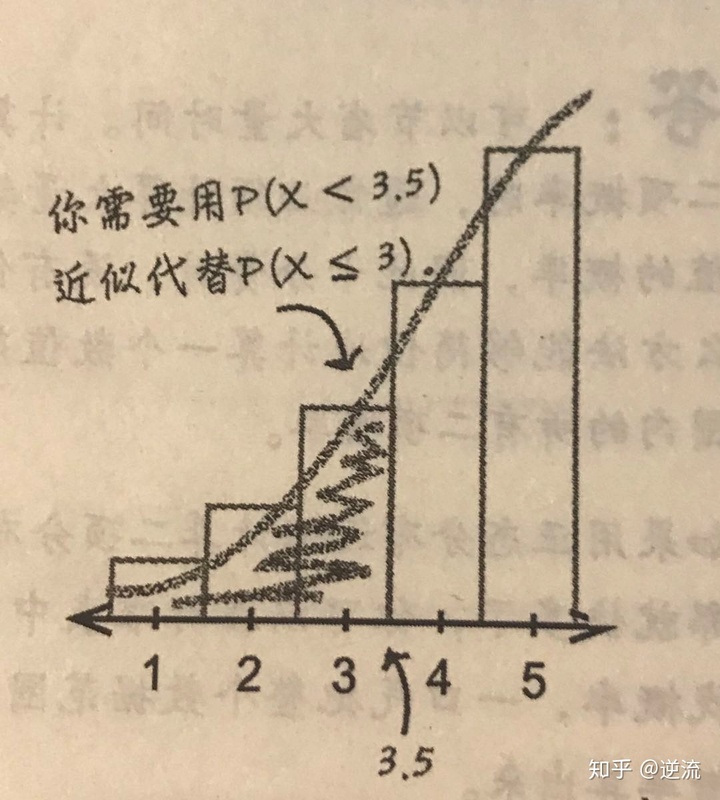
如果使用正太分布求P(X≤a)，则实际上需要计算P（X<a+0.5），以此得出近似值。

【2】≥型概率求解

计算P(X≥b)这种形式的概率时，要确保所选择范围包含离散数值a，在一个连续标度上，离散数值b会减小到（a+0.5）

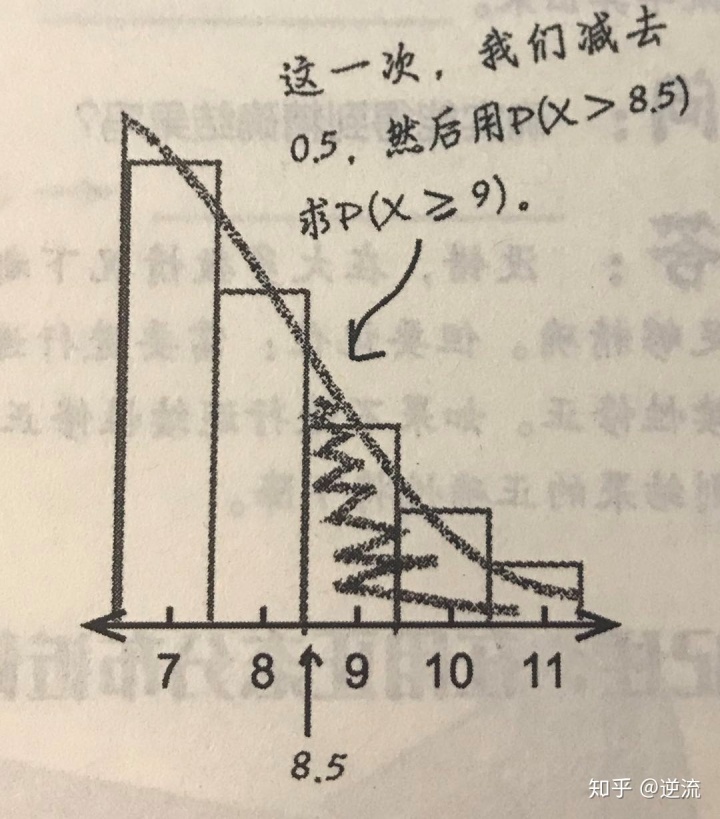
如果使用正太分布求P(X≥b)，则实际上需要计算P（X＞b-0.5），以此得出近似值。

【3】“介于”型概率的求解

计算P(a≤X≤b)这种形式的概率时，需要进行连续修正，确保a和b均包含在内，为此需要将两端范围均扩展0.5

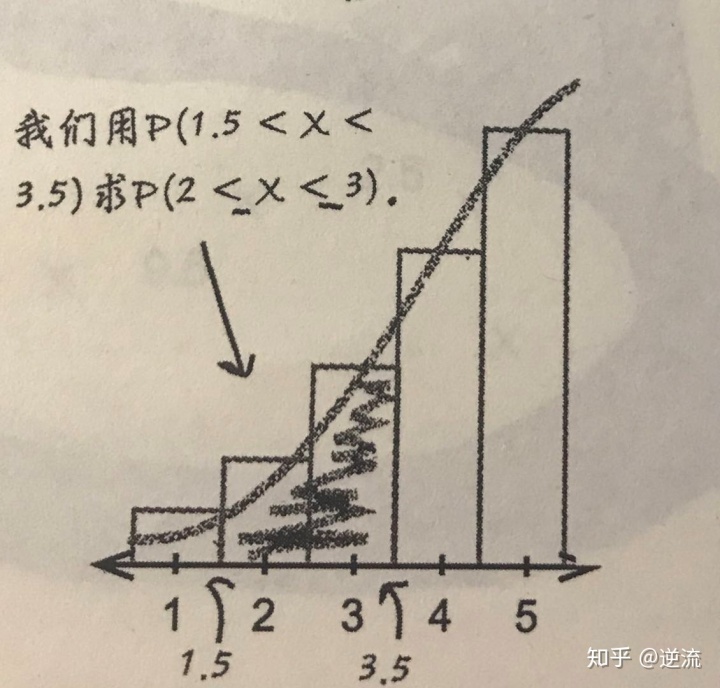
如果使用正太分布求P(a≤X≤b)，则实际上需要计算P（a-0.5<X<b+0.5），以此得出近似值。

总结：

正态分布和泊松分布都能作为二项式分布的近似，那么该用哪一个？

【1】当np>5且nq>5时，则使用正态分布近似代替二项式分布（必须进行连续修正）

【2】当n>50且p<0.1时，则可以使用泊松分布近似代替二项分布

练习题：

回到智力答题比赛，用正态分布代替二项式分布计算，40题答对30题的概率为多少？

本题要求P(X≥30)，n=40，p=0.25，q=0.75

np =10，npq=7.5，满足np>5且nq>5，可以用正态分布计算

我们需要求P(X>29.5)，X~N（np,npq）即X~N（10,7.5）

求标准分

Z = 29.5-10 / 2.74 =7.1

查Z表，得到一个极近似1的概率

P(X<29.5) = 1

P(X>29.5) = 1-1 = 0

所以答对30题以上的概率接近0

正态分布近似代替泊松分布

只要泊松分布形状与正态分布相似时，就可以用正态分布近似代替泊松分布。

当λ很大时，泊松分布与正态分布相似。

如果X~Po(λ) 且 λ >15，则可用X~N(λ,λ)进行近似（必须连续修正）

练习题：

游乐园开通了过山车项目，负责人在网上找了一些统计数据，其中一个网站说，过山车预期故障次数每年40次，负责人认为只要每年故障次数不超过52次，那么项目就可以开通，求概率。

本题中，已知λ =40满足λ >15的前提条件，可以用正态近似法

我们用X~N(40,40)代替泊松分布X~Po(40)，经过修正求P(X<51.5)

求标准分

Z=x-μ / σ = 51.5 - 40 / 6.32 =1.82

查概率表

P(X<51.5) = 0.9656

即一年内故障的次数小于52的概率为0.9656。

要点：

为什么要用正态分布近似代替二项式分布或泊松分布？

使用原来分布计算，结果会更准确，但极其浪费时间，如果想通过二项式分布或泊松分布求出一个数值的范围的概率，就需要求出该数值范围中每一个单独数的概率，相反使用正态分布则可以查找整个范围的概率。

本文归纳总结参考《深入浅出统计学》