感谢性感的傅立叶,让我们可以用 一个方向上的 单位长度的 温度变化量,即,温度梯度,来描述“传热量”,这样一个感性的概念。

什么是温度?
所谓的温度,是对外界环境冷热 程度 的一个 粗略的度量,我们借助一些会顺应这种冷热程度自己膨胀的固体或液体,数量化了外界环境。
但是这种粗略的度量,完全不够描述我们人类的皮肤感受到的“冷”或“热”。(比如,冬天的20℃和夏天的20℃是截然不同的感受)我感受到的寒流侵体,或热流侵体,是由单位时间内的换热量决定的。
而傅立叶就告诉我们,我们可以直接用温度的变化趋势,来描述身处在一个环境中的一个系统(比如,人体,是个敞开系统)所“感受”到的“冷”“热”。
我们人可以做什么?我们想要什么?
人是比较贪心的,
给我一个系统,
尽管我只能测出,或者安排好某一个时刻的系统中每个点的温度。
我也可以对这个系统做做手脚,
比如不许它和外界交换能量(绝热),
比如让它一头不许跟外界交换能量,一头允许交换,
或者,我还可以不允许一头传热,允许一头“自由传热”。
我们管这个时刻叫初始时刻,因为我们手上有这一时刻系统内各个点的温度值,我们用数学语言将它描述成一个函数,叫φ(x)。
我们悄摸摸地给系统做的手脚,就是所谓的“边界条件”。这三种诡计,在进行数学语言描述的时候,分别被归为“第二类边界条件”,“混合边界条件”和“第三类边界条件”。
我们可以仗着自己有傅立叶撑腰,因为他为我发现了如何用温度变化量来描述传热量。借此,我们就可以推导出导热过程的微分方程(这里省略推导,材工基课本儿p139有)。这个微分方程,也就是我们所谓的“泛定方程”了。
微分方程在手,我们感到自己获得了自然界的神谕,可以开始尝试描述这三件事。
我们现在找一根杆子玩儿,我们想对这根杆子做这三种限制。
我们开始语言描述:
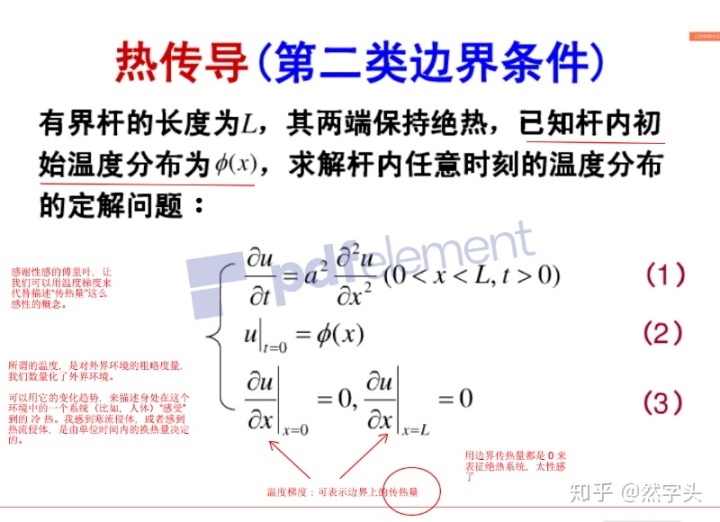

前两种手段还好说,但第三种手段,一头要“自由换热”,这怎么说呢?
有人给【自由换热】下了定义(也就是说,有人用人类惯用的语言来描述了一下这件事,方便我们用数学语言翻译出这件事):
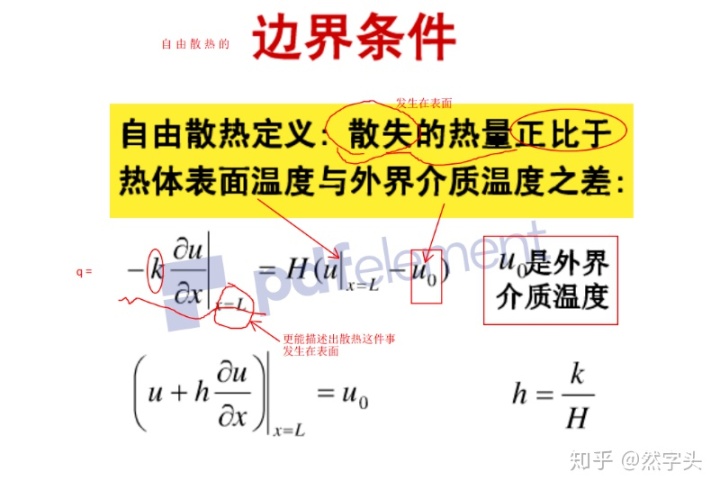








 本文介绍了数学物理方法在解决一维热传导问题中的应用,特别是使用分离变量法来求解不同边界条件下的温度分布。讨论了绝热系统、混合边界条件和自由传热条件下的热传导模型,并引用了顾樵的《数学物理方法》作为参考书目。
本文介绍了数学物理方法在解决一维热传导问题中的应用,特别是使用分离变量法来求解不同边界条件下的温度分布。讨论了绝热系统、混合边界条件和自由传热条件下的热传导模型,并引用了顾樵的《数学物理方法》作为参考书目。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








