KMP算法 LRU算法

KMP算法

KMP算法要解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题。

即可以用来匹配模式字符串，或者寻找最小重复单元 ; 寻找最小重复单元就是计算出字符串的最长公共前缀的长度a，如果 a != 0 && len %(len-a) == 0即找到最小重复单元。

面试官夺命三连

KMP 是啥？KMP 能干啥？手写 KMP ？

Knuth-Morris-Pratt字符串查找算法（简称为KMP算法）可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现，从而避免重新检查先前匹配的字符。 

KMP算法可以实现复杂度由O(n*m)转为O(m+n)

为何简化了时间复杂度： 
充分利用了目标字符串ptr的性质（比如里面部分字符串的重复性，即使不存在重复字段，在比较时，实现最大的移动量）

next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。

*注意最长前缀：是说以第一个字符开始，但是不包含最后一个字符。 比如aaaa相同的最长前缀和最长后缀是aaa。* 

在暴力法中,我们已经知道前面三个字符都是匹配的！（这很重要）。移动过去肯定也是不匹配的！有一个想法，i可以不动，我们只需要移动j即可，：“利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置。”

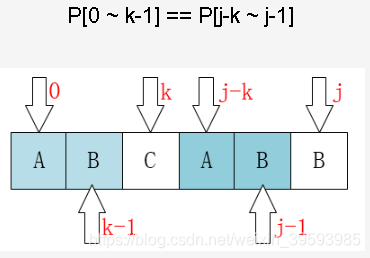
当T[i] != P[j]时

有T[i-j ~ i-1] == P[0 ~ j-1]

由P[0 ~ k-1] == P[j-k ~ j-1]

必然：T[i-k ~ i-1] == P[0 ~ k-1]

公式很无聊，能看明白就行了，不需要记住。

这一段只是为了证明我们为什么可以直接将j移动到k而无须再比较前面的k个字符。

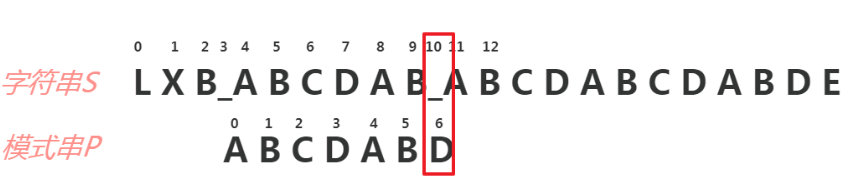
next[j]的值（也就是k）表示，当P[j] != T[i]时，j指针的下一步移动位置。(j指向主串位置 , i指向目标串位置)

public static int[] getNext(String ps) {
    char[] p = ps.toCharArray();//将短字符串转换为字符串数组
    int[] next = new int[p.length];
    next[0] = -1;
    int j = 0;
    int k = -1;
    while (j < p.length - 1) {
       if (k == -1 || p[j] == p[k]) {
           next[++j] = ++k;
       } else {
           k = next[k];
       }
    }
    return next;
}

https://blog.youkuaiyun.com/starstar1992/article/details/54913261/

转自 https://www.cnblogs.com/yjiyjige/p/3263858.html

 public static int kmp(String string, String pattern) {
        char[] s = string.toCharArray();
        char[] p = pattern.toCharArray();
        int len_s = string.length;
        int len_p = pattern.length;
        int i = 0, j = 0;
        int[] next = getNext(pattern);//公共前缀后缀
        while (i < len_s && j < len_p) {
            if (j == -1 || s[i] == p[j]) {
                i++;
                j++;
            } else {
                j = next[j];//在字符串不匹配时，获得此位置的公共前后缀
            }
        }
        if (j == p.length) {
            return i - j;//找到了匹配的字符串，返回位置
        } else {
            return -1;
        }
    }

计算完成next数组之后，我们就可以利用next数组在字符串O中寻找字符串f的出现位置。匹配的代码和求next数组的代码非常相似，因为匹配的过程和求next数组的过程其实是一样的。假设现在字符串f的前i个位置都和从某个位置开始的字符串O匹配，现在比较第i+1个位置。如果第i+1个位置相同，接着比较第i+2个位置；如果第i+1个位置不同，则出现不匹配，我们依旧要将长度为i的字符串分割，获得其最大公共长度next[i]，然后从next[i]继续比较两个字符串。这个过程和求next数组一致，所以可以匹配代码如下（java版）：

 
public void search(String original, String find, int next[]) {
	int j = 0;
	for (int i = 0; i < original.length(); i++) {
		while (j > 0 && original.charAt(i) != find.charAt(j))
			j = next[j];
		if (original.charAt(i) == find.charAt(j))
			j++;
		if (j == find.length()) {
			System.out.println("find at position " + (i - j));
			System.out.println(original.subSequence(i - j + 1, i + 1));
			j = next[j];
		}
	}
//注意 : 每次我们得到一个匹配之后都要对j重新赋值。

改进后 参考 https://blog.youkuaiyun.com/yutianzuijin/article/details/11954939

 
public int[] getNext(String b)
{
	int len=b.length();
	int j=0;
		
	int next[]=new int[len+1];//next表示长度为i的字符串前缀和后缀的最长公共部分，从1开始
	next[0]=next[1]=0;
		
	for(int i=1;i<len;i++)//i表示字符串的下标，从0开始
	{//j在每次循环开始都表示next[i]的值，同时也表示需要比较的下一个位置
		while(j>0&&b.charAt(i)!=b.charAt(j))j=next[j];
		if(b.charAt(i)==b.charAt(j))j++;
		next[i+1]=j;
	}
		
	return next;
}

总结 : 初始化next[0]=next[1]=0 , next()存储的就是最长前缀后缀 , 根据前面的next的值j来求取下一个next(i+1)的值 ;KMP算法 ,在不匹配时, 主串的指针不动 , 目标字符串回溯 j = next[j]; , 

核心在于next数组的计算。

我们求取的next数组表示长度为1到m的字符串f前缀的最大公共长度，所以需要多分配一个空间。而在遍历字符串f的时候，还是从下标0开始(位置0和1的next值为0，所以放在循环外面)，到m-1为止。代码的结构和上面的讲解一致，都是利用前面的next值去求下一个next值。

 

科赫曲线

LRU算法

"明星算法" https://blog.youkuaiyun.com/liewen_/article/details/83150476

FIFO：先进先出调度算法

LRU：最近最久未使用调度算法

两者都是缓存调度算法，经常用作内存的页面置换算法。

参考 https://www.cnblogs.com/yuanninesuns/p/8542024.html

FIFO算法访问序列：1，2，3，4，1，2，5，1，2，3，4，5                    1，2，3先调入内存，内存结构：3      2      1    缺页次数：3                      4调入内存，1调出，  内存结构：4      3      2    缺页次数：4                    1调入内存，2调出，  内存结构：1      4      3    缺页次数：5                    2调入内存，3调出，  内存结构：2      1      4    缺页次数：6                    5调入内存，4调出，  内存结构：5      2      1    缺页次数：7                    1存在，内存结构不改变                    2存在，内存结构不改变                    3调入内存，1调出，  内存结构：3      5      2    缺页次数：8                    4调入内存，2调出，  内存结构：4      3      5    缺页次数：9                    5存在，内存结构不改变             共缺页9次，缺页中断率 ＝ 缺页中断次数 / 总访问页数 ＝ 9 / 12     LRU算法：最近最少使用（Least Recently Used），先看一下调页过程            访问序列：1，2，3，4，1，2，5，1，2，3，4，5                 1，2，3先调入内存，内存结构：3      2      1    缺页次数：3                   4调入内存，1调出，  内存结构：4      3      2    缺页次数：4                 1调入内存，2调出，  内存结构：1      4      3    缺页次数：5                 2调入内存，3调出，  内存结构：2      1      4    缺页次数：6                 5调入内存，4调出，  内存结构：5      2      1    缺页次数：7            到这一步其实和FIFO并没有区别               1调入内存，由于内存中存在1，故没有缺页中断，但由于1最近被访问过，所以要将其位置调换，               使它最后一个被淘汰，内存结构：1      5      2               2调入内存，没有缺页中断，但内存位置要变化，内存结构：2      1      5                   3调入内存，5调出，  内存结构：3      2      1    缺页次数：8                   4调入内存，1调出，  内存结构：4      3      2    缺页次数：9                   5调入内存，2调出，  内存结构：5      4      3    缺页次数：10            共缺页10次，缺页中断率：10/12

编写一段泛型程序来实现LRU缓存? (O(1)复杂度)参考 https://www.cnblogs.com/lzrabbit/p/3734850.html (有多种数据结构的实现方式)

　　对于喜欢Java编程的人来说这相当于是一次练习。给你个提示，LinkedHashMap可以用来实现固定大小的LRU缓存，当LRU缓存已经满了的时候，它会把最老的键值对移出缓存。LinkedHashMap提供了一个称为removeEldestEntry()的方法，该方法会被put()和putAll()调用来删除最老的键值对。当然，如果你已经编写了一个可运行的JUnit测试，你也可以随意编写你自己的实现代码。

import java.util.LinkedHashMap;
import java.util.Map;
 //LinkedHashMap的一个构造函数，当参数accessOrder为true时，即会按照访问顺序排序，最近访问的放在最前，最早访问的放在后面
public LRUCache<K, V> extends LinkedHashMap<K, V> {
  private int cacheSize;
 
  public LRUCache(int cacheSize) {
    super(16, 0.75, true);
    this.cacheSize = cacheSize;
  }
//LinkedHashMap自带的判断是否删除最老的元素方法，默认返回false，即不删除老数据
//我们要做的就是重写这个方法，当满足一定条件时删除老数据 原方法默认返回false 因此要重新方法
  protected boolean removeEldestEntry(Map.Entry<K, V> eldest) {
    return size() >= cacheSize;
  }
}

https://www.cnblogs.com/fkissx/p/4712959.html 其他算法