三维坐标系怎么画_唯心识学061·简单介绍一下球坐标系

简单介绍一下球坐标系

原创： 善欢喜王 唯心识学 2019-02-11

春节假期结束了，我们继续唯心识学的学习。

今天带大家复习一下球坐标系的基本知识，很快我们就要接触到史瓦西度规了。

之所以要用到球坐标系，是因为球坐标系在研究球对称的对象时实在是太方便了。

大家可以想想，若用三维直角坐标系研究球对称对象，将球面上任意一点的坐标用（x、y、z）坐标表示会有多麻烦。用球坐标系就简单多了，一个半径 r ，一个极角 θ ，一个方位角 φ 全部搞定。比如半径 r=1 ，极角 θ=π/4 ，方位角 φ=π/6 ，我们很容易就能想象出这个坐标点在球面上的位置，但是若将这个坐标点换算为三维直角坐标系中的坐标，有几个人能一下子想象出那三个用无理数表示的坐标对应着球面上的哪个点呢？

径向距离（Radial distance）是球面坐标点到球心的距离，用 r 表示。有时为了帮助理解，坐标点与球心的连线也可以直接用 r 表示。

极角（The polar angle）是 z 轴与 r 的夹角，一般用 θ 表示，它的取值范围是 [0,π]，z 轴上任何点的极角都是 0 。

方位角（The azimuth angle）是赤道面（由 x 轴与 y 轴确定的平面）上起始于 x 轴，沿逆时针方向量出的角度，通常用 φ 表示。

可以将球面上的任意一点的三维直角坐标记做 P(x,y,z) ，球坐标记做 P(r,θ,φ) 。

球坐标 P(r,θ,φ) 与直角坐标 P(x,y,z) 之间的转换关系可以表示为：

x=rsinθcosφ

y=rsinθsinφ

z=rcosθ

这是一个非常重要的转换关系。其中 rsinθ 就是图中 zP 到 P 的距离。

将 rsinθ 取 cosφ 就是 x 轴的坐标

将 rsinθ 取 sinφ 就是 y 轴的坐标

将 r 直接取 cosθ 就是 z 轴的坐标

这些内容很直观，一点也不难，读懂它们只需要一些耐心而已。

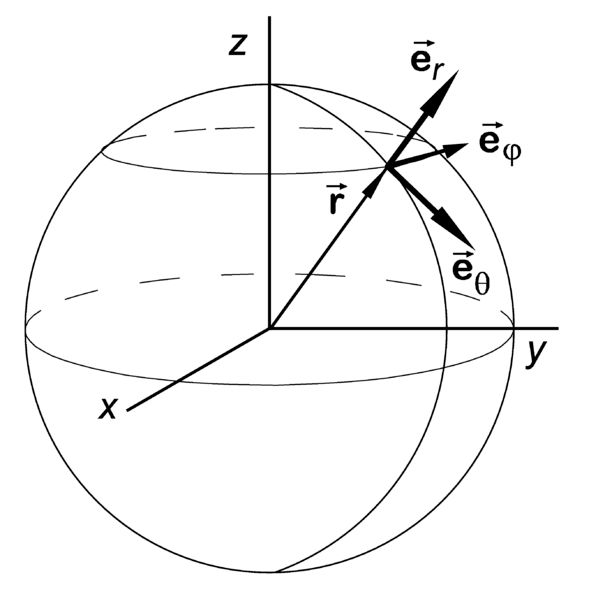
球面上任意一点都存在三个矢量方向，分别是：

1、径向 er

2、极角方向 eθ

3、方位角方向 eφ

若球面上的任意一点 P 存在运动趋势，那么 P 点的瞬时运动方向一定可以用 er、eθ、eφ 的线性组合来表示。

接下来复习一下弧长的概念。（这里只说圆周上的弧长）

我们都知道圆周长的公式为 C=2πR

因为一个圆周的弧度就是2π，所以：

弧长=弧度*半径 ，即 L=αR 。

弧度与角度可不要弄混了，360°是角度，2π是弧度。

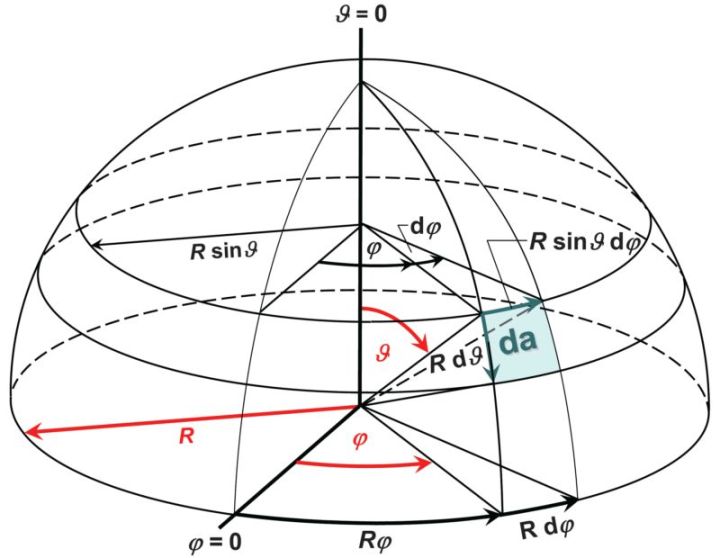
现在假设球面上的 P 存在一个微小的运动趋势，我们应该怎么表示呢？

可以将这个运动趋势分解为三个方向的趋势微元（这里用微分表示），之后再组合就是了。

半径 r 方向的趋势微元显然是 dr 。

极角方向的趋势微元是 rdθ，其中半径 r 是固定的，变化的只有极角 θ 。

方位角方向的趋势微元是 rsinθdφ ，其中 rsinθ 是小圆半径，是固定的，变化的只有方位角 φ 。

所以很显然，组合之后的结果为

dr + rdθ + rsinθdφ

以上内容若能熟练掌握，球坐标系的基础知识就暂时够用了。

想看懂唯心识学中对史瓦西度规的解释，以上这些内容可都是基础。