kkt条件 弱对偶 强对偶_浅谈KKT条件

正在学习机器学习的相关内容，其中用到KKT条件，在这里把自己对于KKT条件的一些理解和运用记录下来

注：本文参考知乎作者Eureka的文章

Eureka：Karush-Kuhn-Tucker (KKT)条件​zhuanlan.zhihu.com

---

1.拉格朗日乘数法

在了解KKT条件之前，先来复习一遍拉格朗日乘数法，拉格朗日乘数法是一种寻找多元函数在起变量收到一个或者多个条件约束时的极值的方法，一般形式如下：

min f(x)

s.t. g(x)=0

定义拉格朗日函数

那么求

可以变成求

通过对

求偏导数,并且将偏导数的值设置为0，那么可以得到一组方程：

其中第一条方程称为定常方程（stationary equation），第二条方程为约束条件。解以上方程组，即可得到在约束条件下函数的最优解

---

2.KKT条件

若将约束条件

扩展为不等式

,那么最优化问题可以表达为

不等式

称为原始可行性（primal feasibility）假设

为满足以上约束条件的最优解，那么我们可以分两种情况讨论：

（1）

，最优解位于约束范围内部,我们称为内部解，这个时候约束条件是无效的

（2）

,最优解落在约束范围的边界上，我们称为边界解，这个时候约束条件是有效的。

这两种情况的最佳解具有不同的必要条件。

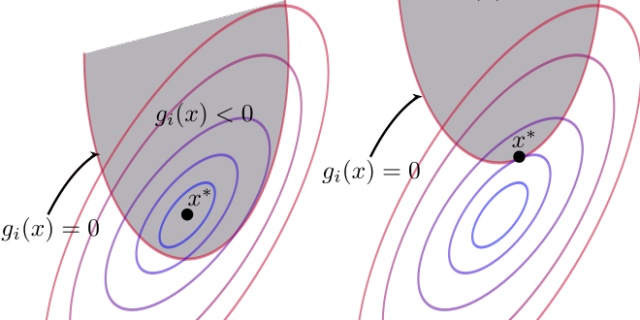
1）内部解：因为约束条件不生效，因为驻点

满足

2)边界解：在约束条件有效的情况下，约束条件不等式变成

, 这个时候形式与之前的拉格朗日乘数法一致。需要注意 是，拉格朗日乘数法的

可正可负，但是这里的

(称为对偶可行性)

因此，不管驻点

位于内部或者边界，都有

成立，称为互补松弛性（complementary slackness）。综合以上的情况，最优解的必要条件包括拉格让日函数

的定常方程式，原始可行式，对偶可行式，以及互补松弛式:

以上的条件合称KKT条件，如果我们要最大化

并且受限于

,那么对偶可行性要改成

, 若果限制条件为

,那么可以通过不等式两遍同时乘以-1，使不等式变为

把上面的结果推广到多个约束等式和约束不等式的情况：

定义拉格朗日函数

对应的KKT条件包括：