极大似然估计_计量丨极大似然估计(1)

答疑

1.极大似然方法把样本独立同分布当成默认假设

极大似然方法不一定要求样本独立同分布但一般统计教材都只讨论独立同分布的情况，目前考试也只涉及独立同分布的题目，可当做默认假设。

2.dlnL/dθ=0方法&定义法求MLE，dlnL/dθ=0是MLE的必要非充分条件

一阶条件只是MLE的必要条件，不是充分条件

满足dlnL/dθ=0的θ还需要满足

①   似然方程dlnL/dθ=0只有唯一解

②   似然函数最大值在参数空间Θ内部达到

这两个条件对指数族都成立(唯一解可以解出来，θ是内点解也很好验证)

不能用一阶导求MLE的情况：

①L(θ|y)不是θ的可微函数甚至不是连续函数时，不能求导

②L(θ|y)对θ的导数恒为正数或负数，即不存在dlnL/dθ=0的点

求导不可行，用定义法，找令L(θ|y)最大的θ即可

         这类定义法的例子常见于均匀分布或带参数示性函数的分布，这类分布支撑集与θ有关，因此L(θ|y)对θ不连续，求出的θ有时会涉及次序统计量

用定义法求MLE的常见分布：

均匀分布、双参数指数分布

3.统计量的一致性(相合性)的证明方法&MLE不一定有相合性，需要满足一定的条件

首先明确一致性的定义

计量里一致性=统计里的弱相合估计=依概率收敛

弱相合性：依概率收敛(convergence in probability)

强相合性：几乎处处收敛(convergence almost surely)

顺便复习一下概率论里4种常用收敛及关系

然后补充一下弱相合估计和强相合估计的证明方法

弱相合估计/一致性的证明

按照定义，弱相合估计要证明依概率收敛，计量里常简写为证

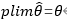
法1：直接用依概率收敛的定义证

证明在n→时为0即可

例子

韦来生例3.3.6证明均匀分布