python绘制直线的垂线_Python，Matplotlib：当数据独立时，在三维打印中绘制垂直线...

在(x，y)平面上有一个随机游走者，在(x，y，z)平面上有一个-log(二元高斯函数)。这两个数据集本质上是独立的。在

我想取样，比如说5对随机行走者，沿着z轴画垂直线，当垂直线“遇到”二元高斯时终止垂直线。在

这是我目前为止的代码：import matplotlib as mpl

import matplotlib.pyplot as plt

import random

import numpy as np

import seaborn as sns

import scipy

from mpl_toolkits.mplot3d import Axes3D

from matplotlib.mlab import bivariate_normal

%matplotlib inline

# Data for random walk

def randomwalk():

mpl.rcParams['legend.fontsize'] = 10

xyz = []

cur = [0, 0]

for _ in range(40):

axis = random.randrange(0, 2)

cur[axis] += random.choice([-1, 1])

xyz.append(cur[:])

# Get density

x, y = zip(*xyz)

data = np.vstack([x,y])

kde = scipy.stats.gaussian_kde(data)

density = kde(data)

# Data for bivariate gaussian

a = np.linspace(-7.5, 7.5, 40)

b = a

X,Y = np.meshgrid(a, b)

Z = bivariate_normal(X, Y)

surprise_Z = -np.log(Z)

# Get random points from walker and plot up z-axis to the gaussian

M = data[:,np.random.choice(20,5)].T

# Plot figure

fig = plt.figure(figsize=(10, 7))

ax = fig.gca(projection='3d')

ax.plot(x, y, 'grey', label='Random walk') # Walker

ax.scatter(x[-1], y[-1], c='k', marker='o') # End point

ax.legend()

surf = ax.plot_surface(X, Y, surprise_Z, rstride=1, cstride=1,

cmap = plt.cm.gist_heat_r, alpha=0.1, linewidth=0.1)

#fig.colorbar(surf, shrink=0.5, aspect=7, cmap=plt.cm.gray_r)

for i in range(5):

ax.plot([M[i,0], M[i,0]],[M[i,1], M[i,1]], [0,10],'k--',alpha=0.8, linewidth=0.5)

ax.set_zlim(0, 50)

ax.set_xlim(-10, 10)

ax.set_ylim(-10, 10)

产生

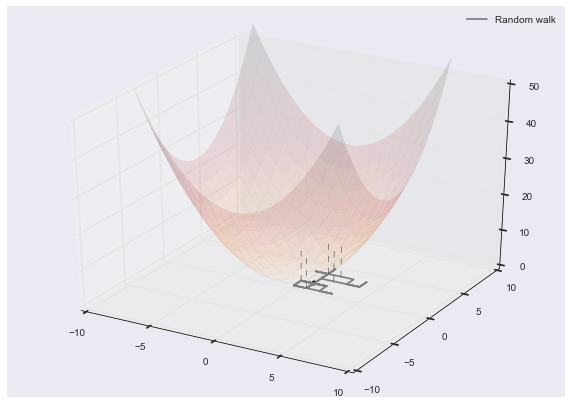
正如你所看到的，我正在努力解决的唯一问题是，当垂直线满足适当的Z值时，如何终止它们。欢迎有任何想法！在