运筹学c语言实现dijkstra算法求解图的最短路径,Dijkstra算法 c语言实现

Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。

Dijkstra算法是很有代表性的最短路算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。

其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。

初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。

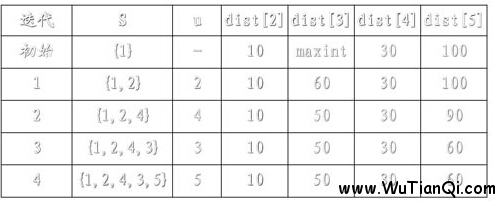
例如，对下图中的有向图，应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。

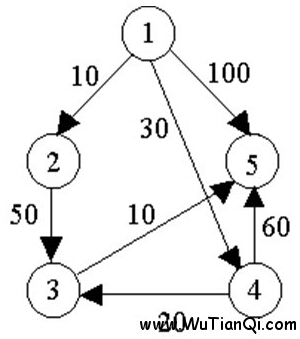
Dijkstra算法的迭代过程：

#include

#include

#include

#define X 10000

#define VertexNum 7 //实际上共有六个顶点(1---6)

#define EdgeNum 9

int Graph[VertexNum][VertexNum] =

//0 1 2 3 4 5 6

{ X, X, X, X, X, X, X, //0

X, X, 6, 3, X, X, X, //1

X, X, X, X, 5, X, X, //2

X, X, 2, X, 3, 4, X, //3

X, X, X, X, X, X, 3, //4

X, X, X, X, 2, X, 5, //5

X, X, X, X, X, X, X //6

};

int Visited[VertexNum];

in