多普勒频移公式_多普勒效应及超声应用（含公式推导）

       1842年奥地利物理学家多普勒(Doppler)发现一种物理现象：当声源与声波接收器处于相对运动时，接收器接收到的声源频率不同于声源发射的频率，且频率的变化与二者的相对运动速度有关。这种现象称为多普勒效应，频率的改变量称作多普勒频移。

如图所示，A为喇叭(声源)，B为耳朵(接收器)。

简单列举4种情况

1. A与B均相对不动。设A发射出波长为λ的声波，以速度c向前传播并被B接收，1秒后声波传过B的距离为c。此时B接收的声波频率为  

                      

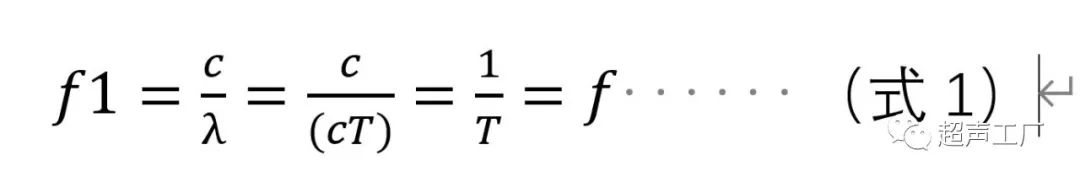
此时f1=f，无多普勒效应。

2. A不动，B以速度V朝向A运动。此时，声波在单位时间内通过B的距离等效为c+V，则B接收到的频率为

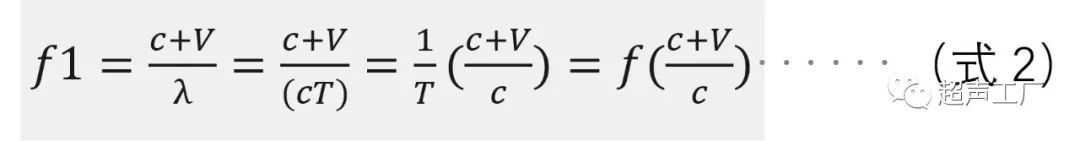
即f1＞f，接收频率比发射频率高。

3. B不动，A以速度U朝向B运动。此时，A在一个振动周期(T)的时间内向B运动了TU距离，这等效于使波长(λ)变短，呈λ1，即

λ1=λ-TU=Tc-TU=T(c-U)

则B接收的声波频率为

即f1＞f，接收频率比发射频率高。

4. A与B各以速度U和V同时做相向运动。由式2和3可得，

  即f1＞f，如果V和U取负值，即声源和接收器均朝远离方向运动，则f1＜f，即接收的声波频率降低

在超声诊断中，发射器和接收器都近似位于同一位置。如图所示，

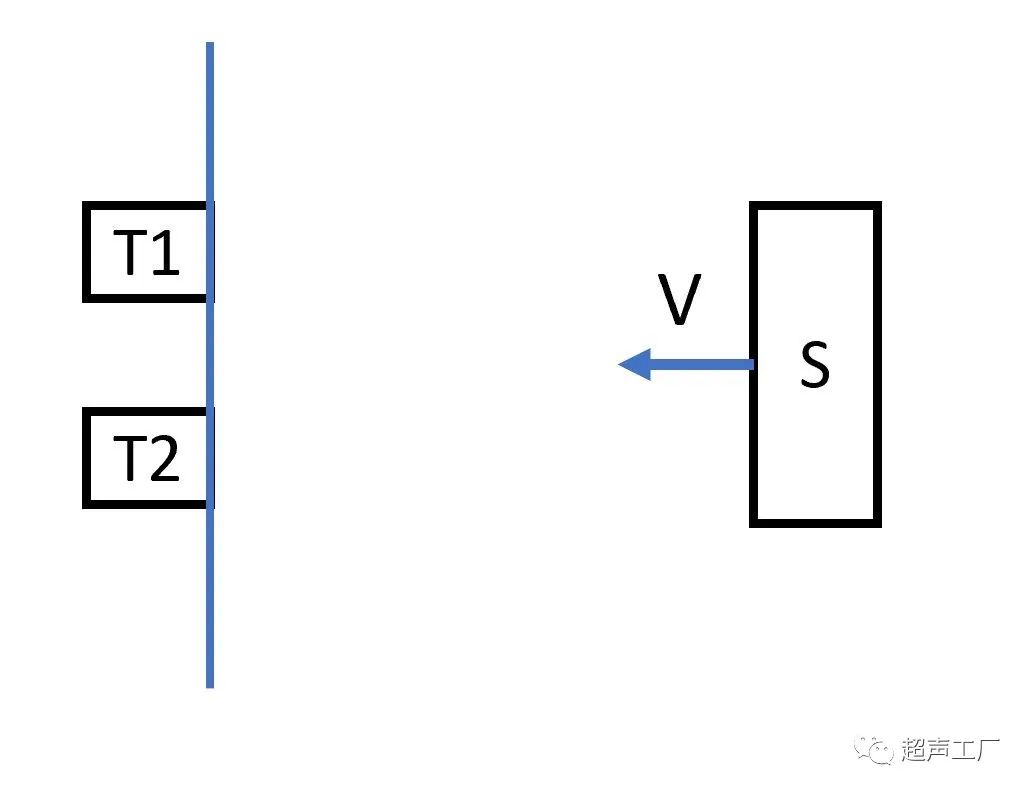
发射器T1发出频率为f的超声波，靶体s接收的频率为fs

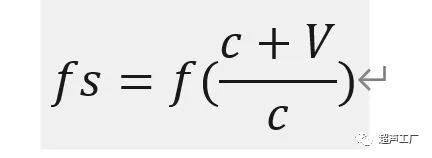
该声波经s反射后，由T2接收器接收，T2接收的频率f2为

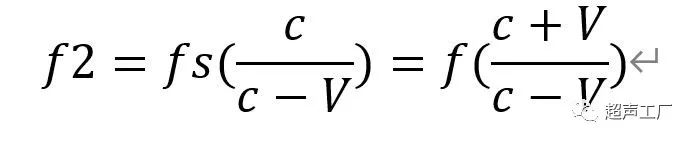
T2除了接收到f2的声波外，还有T1发射的f信号耦合过来，其差频实际上就是多普勒频移fd，

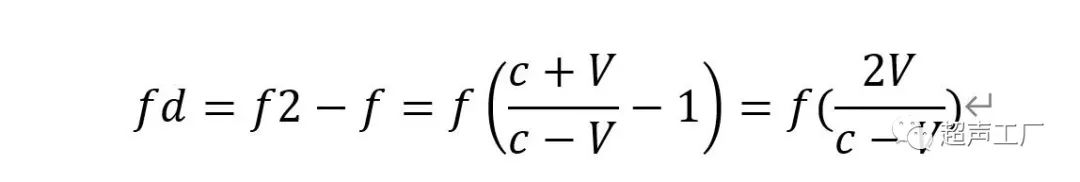
因为通常c＞＞V，故上式可写成

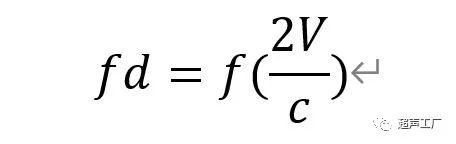
在临床超声诊断中，声束方向一般都与血流方向呈一定角度，如图所示，

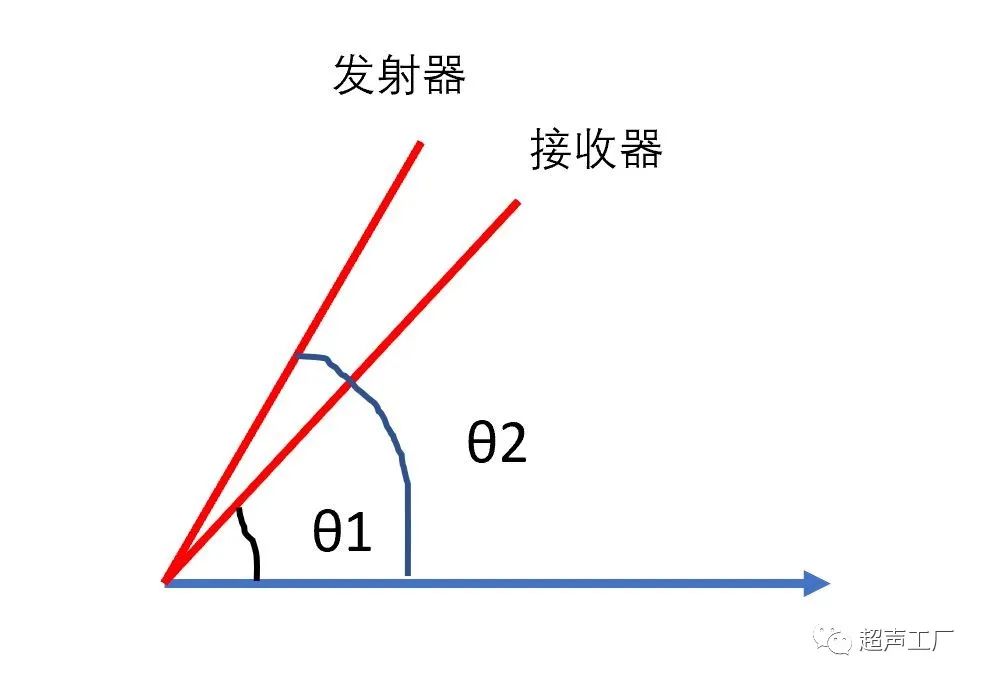
 利用θ角度校正后，

因为T1与T2很靠近，所以θ1=θ2，

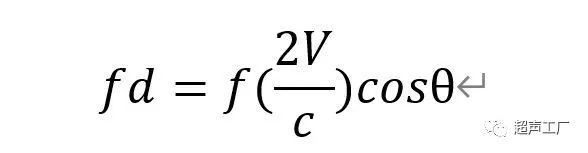
上式就是常用的从多普勒频移(fd)测量靶物体速度(V)的基本公式。

厂长直言：

据说曾经考过多普勒公式的推导，这个确实不容易全部记下来，我认为记住

1. fd=2fV/(c-V)

2. c＞＞V，就把分母里的V去掉了

3. 如果有角度，就再乘cos

参考文献：临床超声鉴别诊断学，贾泽清主编，江苏科学技术出版社